题目内容

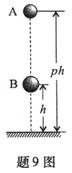
如题9图所示,在同一竖直平面上, 质量为2m的小球静止在光滑斜面底部的压缩弹簧的顶端,此时小球距斜面顶端的高度为.解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时球的速度恰好水平)与静止悬挂在此处的小球发生弹性碰撞,碰撞后球刚好能摆到与悬点同一高度,球沿水平方向抛射落在水平面上的点, 点的投影与的距离为.已知球质量为,悬绳长,视两球为质点,重力加速度为,不计空气阻力.求:

(1)球在两球碰撞后瞬间受到悬绳拉力的大小.

(2)球在两球碰撞前瞬间的速度大小.

(3)弹簧的弹力对球所做的功.　　

⑴设球B在两球碰撞后一瞬间的速度大小为,则由动能定理得.（2分）由牛顿第二定律得（2分）

 ⑵设球A在两球碰撞前一瞬间的速度大小为，球A在两球碰撞后一瞬间的速度大小为,碰撞过程中满足动量守恒定律：；（2分）

机械能守恒定律  （2分）  得，（1分）     .（1分）

⑶ 碰后球A做平抛运动，设碰后一瞬间球A距的高度为：，（2分）

得（1分）

弹簧将球A弹起到A碰B的过程中，由功能原理：（3分）

得W弹=.（2分）

练习册系列答案
相关题目
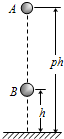精英家教网在一种新的“子母球”表演中，让同一竖直线上的小球A和小球B，从距水平地面高度为ph（p＞1）和h的地方同时由静止释放，如题9图所示．球A的质量为m，球B的质量为3m．设所有碰撞都是弹性碰撞，重力加速度大小为g，忽略球的直径、空气阻力及碰撞时间．
（1）求球B第一次落地时球A的速度大小；
（2）若球B在第一次上升过程中就能与球A相碰，求p的取值范围；
（3）在（2）情形下，要使球A第一次碰后能到达比其释放点更高的位置，求p应满足的条件．

选做题(请从A、B和C三小题中选定两小题作答，如都作答，则按A、B两小题评分．)

A．(选修模块3-3)

（1）下列说法正确的是                                            （       ）

A．熵是物体内分子运动无序程度的量度

B．由氢气的摩尔体积和每个氢分子的体积可估算出阿伏加德罗常数

C．满足能量守恒定律的客观过程都不是可以自发进行的

D．液体表面层的分子比液体内部的分子有更大的分子势能

（2） 一定质量的理想气体由状态A经状态B变化到状态C的p-V图象如图所示．在由状态A变化到状态B的过程中，理想气体的温度          （填“升高”、“降低”或“不变”）．在由状态A变化到状态C的过程中，理想气体吸收的热量       它对外界做的功（填“大于”、“小于”或“等于”）．

（3）已知阿伏加德罗常数为6.0×1023mol-1，在标准状态（压强p0=1atm、温度t0=0℃）下任何气体的摩尔体积都为22.4l，设第（2）问中理想气体在状态A下的温度为0℃，求该气体的分子数．（计算结果取两位有效数字）

B．(选修模块3-4)

（1）以下说法中正确的是                                           (      )

A．拍摄玻璃橱窗内的物品时，往往在镜头前加一个偏振片以增加透射光的强度

B．全息照片往往用激光来拍摄，主要是利用了激光的相干性

C．根据宇宙大爆炸学说，遥远星球发出的红光被地球接收到时可能是红外线

D．超声波可以在真空中传播

（2）平行光a垂直射向一半径为R的玻璃半球的平面，其截面如图所示，发现只有P、Q之间所对圆心角为60°的球面上有光射出，则玻璃球对a光的折射率为         ，若仅将a平行光换成b平行光，测得有光射出的范围增大，设a、b两种色光在玻璃球中的速度分别为va和vb，则va        vb（选填“>”、“<”或“=”）．

（3）在均匀介质中选取平衡位置在同一直线上的9个质点，相邻两质点间的距离均为0.1m，如图(a)所示．一列横波沿该直线向右传播，t=0时到达质点1，质点1开始向下运动，振幅为0.2m，经过时间0.3s第一次出现如图（b）所示的波形．试写出质点1的振动方程．

C．(选修模块3-5)

（1）下列说法正确的有                                               （    ）

A．卢瑟福的α粒子散射实验可以估测原子核的大小

B．氢原子辐射出一个光子后，氢原子的电势能增大，核外电子的运动加速度增大

C．物质波是一种概率波，在微观物理学中不可以用“轨迹”来描述粒子的运动

D．若氢原子从 n = 6 能级向 n = 1 能级跃迁时辐射出的光不能使某金属发生光电效应，则氢原子从 n = 6 能级向 n = 2 能级跃迁时辐射出的光能使该金属发生光电效应

（2）正电子发射计算机断层显象(PET)的基本原理是：将放射性同位素注入人体，在人体内衰变放出的正电子与人体内的负电子相遇而湮灭，转化为一对γ光子，被探测器探测到，并经计算机处理后产生清晰的图象．根据PET的原理，在人体内衰变的方程式是                ；在PET中，的主要用途是作为               ．

（3）如图所示，质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动，并发生对心碰撞，碰后m2被右侧墙壁原速弹回，又与m1碰撞，再一次碰撞后两球都静止．求第一次碰后m1球速度的大小.

选做题(请从A、B和C三小题中选定两小题作答，如都作答，则按A、B两小题评分．)
A．(选修模块3-3)
（1）下列说法正确的是                                           （      ）
A．熵是物体内分子运动无序程度的量度
B．由氢气的摩尔体积和每个氢分子的体积可估算出阿伏加德罗常数
C．满足能量守恒定律的客观过程都不是可以自发进行的
D．液体表面层的分子比液体内部的分子有更大的分子势能
（2）一定质量的理想气体由状态A经状态B变化到状态C的p-V图象如图所示．在由状态A变化到状态B的过程中，理想气体的温度         （填“升高”、“降低”或“不变”）．在由状态A变化到状态C的过程中，理想气体吸收的热量      它对外界做的功（填“大于”、“小于”或“等于”）．

（3）已知阿伏加德罗常数为6.0×1023mol-1，在标准状态（压强p0=1atm、温度t0=0℃）下任何气体的摩尔体积都为22.4l，设第（2）问中理想气体在状态A下的温度为0℃，求该气体的分子数．（计算结果取两位有效数字）
B．(选修模块3-4)
（1）以下说法中正确的是                                           (      )
A．拍摄玻璃橱窗内的物品时，往往在镜头前加一个偏振片以增加透射光的强度
B．全息照片往往用激光来拍摄，主要是利用了激光的相干性
C．根据宇宙大爆炸学说，遥远星球发出的红光被地球接收到时可能是红外线
D．超声波可以在真空中传播
（2）平行光a垂直射向一半径为R的玻璃半球的平面，其截面如图所示，发现只有P、Q之间所对圆心角为60°的球面上有光射出，则玻璃球对a光的折射率为        ，若仅将a平行光换成b平行光，测得有光射出的范围增大，设a、b两种色光在玻璃球中的速度分别为va和vb，则va       vb（选填“>”、“<”或“=”）．

（3）在均匀介质中选取平衡位置在同一直线上的9个质点，相邻两质点间的距离均为0.1m，如图(a)所示．一列横波沿该直线向右传播，t=0时到达质点1，质点1开始向下运动，振幅为0.2m，经过时间0.3s第一次出现如图（b）所示的波形．试写出质点1的振动方程．

C．(选修模块3-5)
（1）下列说法正确的有                                              （   ）
A．卢瑟福的α粒子散射实验可以估测原子核的大小
B．氢原子辐射出一个光子后，氢原子的电势能增大，核外电子的运动加速度增大
C．物质波是一种概率波，在微观物理学中不可以用“轨迹”来描述粒子的运动
D．若氢原子从 n =" 6" 能级向 n =" 1" 能级跃迁时辐射出的光不能使某金属发生光电效应，则氢原子从 n =" 6" 能级向 n =" 2" 能级跃迁时辐射出的光能使该金属发生光电效应
（2）正电子发射计算机断层显象(PET)的基本原理是：将放射性同位素注入人体，在人体内衰变放出的正电子与人体内的负电子相遇而湮灭，转化为一对γ光子，被探测器探测到，并经计算机处理后产生清晰的图象．根据PET的原理，在人体内衰变的方程式是               ；在PET中，的主要用途是作为              ．
（3）如图所示，质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动，并发生对心碰撞，碰后m2被右侧墙壁原速弹回，又与m1碰撞，再一次碰撞后两球都静止．求第一次碰后m1球速度的大小.

在一种新的“子母球”表演中，让同一竖直线上的小球A和小球B，从距水平地面高度为ph（p＞1）和h的地方同时由静止释放，如题9图所示。球A的质量为m，球B的质量为3m。设所有碰撞都是弹性碰撞，重力加速度大小为g，忽略球的直径、空气阻力及碰撞时间。

  （1）求球B第一次落地时球A的速度大小；

  （2）若球B在第一次上升过程中就能与球A相碰，求p的取值范围；

  （3）在（2）情形下，要使球A第一次碰后能到达比其释放点更高的位置，求p应满足的条件。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网