题目内容
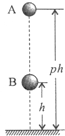
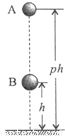
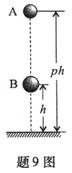
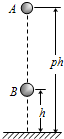 在一种新的“子母球”表演中,让同一竖直线上的小球A和小球B,从距水平地面高度为ph(p>1)和h的地方同时由静止释放,如题9图所示.球A的质量为m,球B的质量为3m.设所有碰撞都是弹性碰撞,重力加速度大小为g,忽略球的直径、空气阻力及碰撞时间.
在一种新的“子母球”表演中,让同一竖直线上的小球A和小球B,从距水平地面高度为ph(p>1)和h的地方同时由静止释放,如题9图所示.球A的质量为m,球B的质量为3m.设所有碰撞都是弹性碰撞,重力加速度大小为g,忽略球的直径、空气阻力及碰撞时间.(1)求球B第一次落地时球A的速度大小;
(2)若球B在第一次上升过程中就能与球A相碰,求p的取值范围;
(3)在(2)情形下,要使球A第一次碰后能到达比其释放点更高的位置,求p应满足的条件.
分析:(1)A、B均做自由落体运动,求出B球的下降时间,便可得到A球的速度
(2)要想在上升阶段两球相碰,临界情况是B刚好反跳回到出发点时与A相碰,据此求出A球的最大高度
(3)要使球A第一次碰后能到达比其释放点更高的位置,临界情况是A与B碰后,A球速度恰好等大反向,由弹性碰撞过程动量守恒可求得碰前vB=3vA,
(2)要想在上升阶段两球相碰,临界情况是B刚好反跳回到出发点时与A相碰,据此求出A球的最大高度
(3)要使球A第一次碰后能到达比其释放点更高的位置,临界情况是A与B碰后,A球速度恰好等大反向,由弹性碰撞过程动量守恒可求得碰前vB=3vA,
解答:解:(1)AB 两球均做自由落体,在B落地过程中运动完全一致,设速度为v0,由运动学公式得: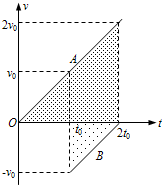
=2gh
故,
=
(2)要想在B上升阶段两球相碰,临界情况是B刚好反跳到出发点时与A相碰,两物体的v-t图象如右图;
阴影部分面积之和就是A的下落高度和B的反跳高度之和ph,故有ph=5h,故p=5
(3)要使球A第一次碰后能到达比其释放点更高的位置,则临界条件是碰后A球速度恰好等大反向,两物体的v-t图象如下图,由弹性碰撞可得碰撞前后,动量守恒,规定向上为正方向,设碰后B球继续向上运动,则:
3mvB-mvA=3mv′B+mvA
由于是弹性碰撞,由碰撞前后能量守恒得:
×3
+
=
×3
+
解得:
=
故必有v′B=-vB
联立以上可得:
vA=3vB
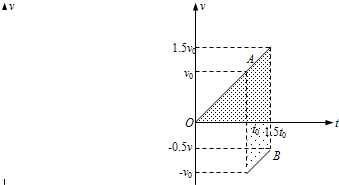
从图象可以看出阴影部分面积之和就是A的下落高度和B的反跳高度之和,故ph=3h,故p=3
答:(1)B第一次落地时球A的速度为
(2)若球B在第一次上升过程中就能与球A相碰,则1<p<5
(3)在(2)情形下,要使球A第一次碰后能到达比其释放点更高的位置,求p应满足1<p<3

| v | 2 0 |
故,
| v | 0 |
| 2gh |
(2)要想在B上升阶段两球相碰,临界情况是B刚好反跳到出发点时与A相碰,两物体的v-t图象如右图;
阴影部分面积之和就是A的下落高度和B的反跳高度之和ph,故有ph=5h,故p=5
(3)要使球A第一次碰后能到达比其释放点更高的位置,则临界条件是碰后A球速度恰好等大反向,两物体的v-t图象如下图,由弹性碰撞可得碰撞前后,动量守恒,规定向上为正方向,设碰后B球继续向上运动,则:
3mvB-mvA=3mv′B+mvA
由于是弹性碰撞,由碰撞前后能量守恒得:
| 1 |
| 2 |
| mv | 2 B |
| 1 |
| 2 |
| ×mv | 2 A |
| 1 |
| 2 |
| mv′ | 2 B |
| 1 |
| 2 |
| mv | 2 A |
解得:
| v | 2 B |
| v′ | 2 B |
故必有v′B=-vB
联立以上可得:
vA=3vB

从图象可以看出阴影部分面积之和就是A的下落高度和B的反跳高度之和,故ph=3h,故p=3
答:(1)B第一次落地时球A的速度为
| 2gh |
(2)若球B在第一次上升过程中就能与球A相碰,则1<p<5
(3)在(2)情形下,要使球A第一次碰后能到达比其释放点更高的位置,求p应满足1<p<3
点评:抓住碰撞前后动量守恒、能量守恒,巧妙利用图象,增强直观性,本题难度较大,对学生的思维有挑战

练习册系列答案
相关题目