题目内容
如图，绝缘水平面AB上方，MN左侧存在着水平向右的匀强电场，场强为E＝500v/m,MN和PQ之间存在着方向水平垂直纸面向里的匀强磁场，且边界MN上即无电场，将质量为m1＝0.02kg，带电量为q1＝2×10-4C的表面绝缘的物块a（视作质点）自距离MN为L＝2m的A点由静止释放，物块A向右加速，并与放置在MN边界上质量为m2＝0.06kg，带电量为q2＝6×10-2C表面绝缘的物块b发生没有机械能损失的碰撞，已知二者与水平面间的动磨擦因数均为μ＝0.1，最终发现物块b沿水平面穿出边界PQ后在无场区又运动了2s后停止运动, (g=10m/s2)，不计两物块间的库仑力，据此求解下列问题
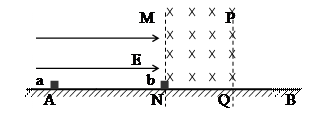
小题1: （1） 磁场的磁感应强度大小B。
小题2: （2） 物块a再次返回边界MN时的速度大小v。
小题1: （1） 磁场的磁感应强度大小B。
小题2: （2） 物块a再次返回边界MN时的速度大小v。
小题1: (1)B=5T
小题2: (2)v=1.63m/s
带电粒子在复合场(电场磁场和重力场)中的运动问题。考查的具体知识点有：动能定理，动量守恒，左手定则等，属综合能力题，含未知过程，难度0.5。
小题1: (1) 物块在向右加速的过程中，
由动能定理得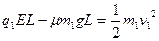
代入数据得
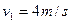
物块ab碰撞过程，由动量守恒得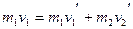
由机械能守恒得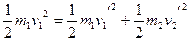
两式联立代入数据得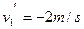
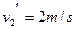即物块A向左返回，而B将以2m/s的速度向右运动。物块B沿水平面向右运动穿出磁场时的速度大小仍为2m/s,r所以可知，物块B在磁场中做匀速直线运动，即物块B将不受磨擦，由竖直方向上受力平衡得
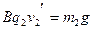
代入有关数据，得磁场的磁感应强度为B=5T。
小题1: (2) 由以上计算可知，物块A一定会再次返回边界MN，
物块A在向左运动的过程中，由牛顿第二定律得，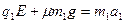
由运动学公式得物块A向左运动的距离为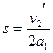
物块A向右运动到边界MN的过程中，有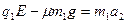
同理有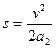
几式联立可得
.
小题1: (1) 物块在向右加速的过程中，
由动能定理得
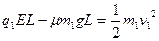代入数据得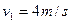物块ab碰撞过程，由动量守恒得
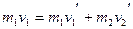
由机械能守恒得
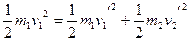
两式联立代入数据得
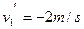
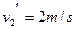即物块A向左返回，而B将以2m/s的速度向右运动。物块B沿水平面向右运动穿出磁场时的速度大小仍为2m/s,r所以可知，物块B在磁场中做匀速直线运动，即物块B将不受磨擦，由竖直方向上受力平衡得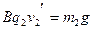代入有关数据，得磁场的磁感应强度为B=5T。
小题1: (2) 由以上计算可知，物块A一定会再次返回边界MN，
物块A在向左运动的过程中，由牛顿第二定律得，
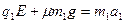
由运动学公式得物块A向左运动的距离为
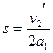
物块A向右运动到边界MN的过程中，有
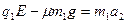
同理有
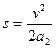
几式联立可得
.
练习册系列答案
综合自测系列答案
相关题目
