Question

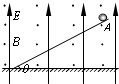在互相垂直的匀强磁场和匀强电场中固定放置一光滑的绝缘斜面，其倾角为θ．设斜面足够长，磁场的磁感应强度为B，方向垂直纸面向外，电场方向竖直向上，如图所示．一质量为m、带电量为q的小球放在斜面的最高点A，小球对斜面的压力恰好为零．在释放小球的同时，将电场方向迅速改为竖直向下，电场强度的大小不变，重力加速度为g．求：
（1）电场强度的大小；
（2）小球沿斜面下滑的速度v为多大时，小球对斜面的压力再次为零；
（3）小球从释放到离开斜面共经过多长时间？

Answer 1

分析：（1）小球放在最高点A，电场竖直向上时，小球对斜面的压力恰好为零，电场力与重力平衡，有mg=Eq，即可求得E．
（2）当电场竖直向下时，小球受到向下的力为2mg；当小球恰好离开斜面时，斜面对小球的弹力恰好为零，根据在垂直于斜面的方向上合力为零，由此可求出此时的速度；
（3）经受力分析可知，小球在沿斜面方向上合力不变，故沿斜面做匀加速直线运动，由运动学公式可求出运动时间．

解答：解：（1）小球放在最高点A时，小球对斜面的压力恰好为零，有 mg=Eq
解得 E=

mg

q

（2）电场反向后，小球做匀加速运动，所受洛伦兹力将增大，当小球对斜面的压力再次为零时，斜面对小球的支持力为零，有 （mg+Eq）cosθ=Bqv
解得 v=

2mgcosθ

qB

（3）小球在平行于斜面方向上只受重力和电场力的分力作用，有
（mg+Eq）sinθ=ma
则得 a=2gsinθ
所以小球做匀加速运动，小球从释放到离开斜面一共历时 t=

v

a

=

mcotθ

Bq

答：
（1）电场强度的大小为

mg

q

；
（2）小球沿斜面下滑的速度v为

2mgcosθ

qB

时，小球对斜面的压力再次为零；
（3）小球从释放到离开斜面共经过的时间为

mcotθ

Bq

．

点评：该题考查了带电物体在复合场中的运动情况，解决此类问题要求我们要对带电物体进行正确的受力分析，要注意找出当小球离开斜面时的受力情况是解决该题的关键．