题目内容
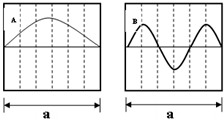
 A、B两列简谐波在某时刻的波形如图所示,经过t=TA时间(TA为波A的周期),两波再次出现如图波形,则两波的波速之比不可能的是( )
A、B两列简谐波在某时刻的波形如图所示,经过t=TA时间(TA为波A的周期),两波再次出现如图波形,则两波的波速之比不可能的是( )分析:通过波形图可知,两列波的波长为为3:1,经过t=TA时间(TA为波A的周期),两波再次出现如图所示波形,知A波向前平移一个波长,而B波向前平移自身波长的整数倍.
解答:解:由图可知
=3,经过t=TA时间有:vATA=λA,vBTA=nλB,(n为大于0的整数)得
=
.
当n=1时,vA:vB=3:1;当n=2时,vA:vB=3:2.当n=4时,vA:vB=1:2.当n=3时,vA:vB=1:1.故A、C、D正确,B错误.
本题选不可能的,故选B.
| λA |
| λB |
| vA |
| vB |
| 3 |
| n |
当n=1时,vA:vB=3:1;当n=2时,vA:vB=3:2.当n=4时,vA:vB=1:2.当n=3时,vA:vB=1:1.故A、C、D正确,B错误.
本题选不可能的,故选B.
点评:解决本题的关键从图中能得出两列波的波长比,以及知道波再次出现以前的波形,则波经过的时间是周期的整数倍,波形移动的距离是波长的整数倍.

练习册系列答案
相关题目
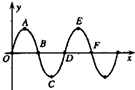 如图所示,为一列简谐波在某一时刻的波形图,以下说法正确的是( )
如图所示,为一列简谐波在某一时刻的波形图,以下说法正确的是( )| A、A、C两点的振幅相同 | B、B点此时的振动方向一定沿y轴正方向 | C、A、C两点的位移相同 | D、在同一振动图象中画出A、B两质点的振动图象完全一样 |