题目内容
12.A球由塔顶自由落下,当落下距离为a时,B球自距塔顶b处开始自由下落,两球恰好同时落地,求塔的高度.分析 A球下落高度a的时间即为A球下落的时间比B球下落的时间长的时间,分别对AB两球运用自由落体位移时间公式即可解题
解答 解:根据h=$\frac{1}{2}g{t}^{2}$得:
t=$\sqrt{\frac{2a}{g}}$,
设塔高h,则b球下落的时间为:tb=$\sqrt{\frac{2(h-b)}{g}}$ ①
对a球有:h=$\frac{1}{2}g({t}_{a}+{t}_{b})^{2}$ ②
由①②解得:h=$\frac{(a+b)^{2}}{4a}$.
答:塔的高度为$\frac{{(a+b)}^{2}}{4a}$.
点评 解决本题的关键知道自由落体运动的运动规律,结合运动学公式灵活求解,基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列描述的匀变速直线运动中,可能存在的是( )
| A. | 速度变化很大,加速度却很小 | |
| B. | 速度变化的方向为正,加速度方向为负 | |
| C. | 速度方向为正,加速度方向为负 | |
| D. | 速度越来越大,加速度越来越小 |
18.一个物体从静止开始以加速度a做匀加速直线运动,经过时间t后改为做匀速运动,又经过时间2t后改为做匀减速运动,再经过时间3t刚好静止.下列说法正确的是( )
| A. | 在6t时间内的总位移大小为4at2 | |
| B. | 在6t时间内的平均速度大小为at | |
| C. | 匀减速运动的加速度大小为3a | |
| D. | 匀减速运动过程中的平均速度大小为0.5at |
19. 一匀强磁场,磁场方向垂直于纸面,规定垂直纸面向里的方向为正,在磁场中有一细金属圆环,线圈平面位于纸面内,如图甲所示.现令磁感应强度B随时间t变化,先按图乙中所示的Oa图线变化,后来又按图线bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流,则( )
一匀强磁场,磁场方向垂直于纸面,规定垂直纸面向里的方向为正,在磁场中有一细金属圆环,线圈平面位于纸面内,如图甲所示.现令磁感应强度B随时间t变化,先按图乙中所示的Oa图线变化,后来又按图线bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流,则( )
 一匀强磁场,磁场方向垂直于纸面,规定垂直纸面向里的方向为正,在磁场中有一细金属圆环,线圈平面位于纸面内,如图甲所示.现令磁感应强度B随时间t变化,先按图乙中所示的Oa图线变化,后来又按图线bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流,则( )
一匀强磁场,磁场方向垂直于纸面,规定垂直纸面向里的方向为正,在磁场中有一细金属圆环,线圈平面位于纸面内,如图甲所示.现令磁感应强度B随时间t变化,先按图乙中所示的Oa图线变化,后来又按图线bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流,则( )| A. | E1>E2,I1沿逆时针方向,I2沿顺时针方向 | |
| B. | E1<E2,I1沿逆时针方向,I2沿顺时针方向 | |
| C. | E1<E2,I1沿顺时针方向,I2沿逆时针方向 | |
| D. | E2>E3,I2沿顺时针方向,I3沿顺时针方向 |
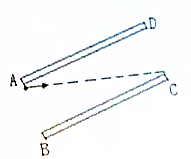 如图所示,平行板电容器的两个极板AD与BC的长度为4cm,它们相距3cm,上极板的A端与下极板的C端在同一水平面上,两极板与一直流电源相连,若一质量为4×10-3kg、带电量为-3×10-7C的带电微粒从A点进入电容器间电场后恰能沿图中所示的AC连线做直线运动,且刚好能够到达C点(重力加速度取10m/s2)试求:
如图所示,平行板电容器的两个极板AD与BC的长度为4cm,它们相距3cm,上极板的A端与下极板的C端在同一水平面上,两极板与一直流电源相连,若一质量为4×10-3kg、带电量为-3×10-7C的带电微粒从A点进入电容器间电场后恰能沿图中所示的AC连线做直线运动,且刚好能够到达C点(重力加速度取10m/s2)试求: 如图所示,实线为一简谐波该时刻的波形图,虚线是该波经0.2s后的波形图.
如图所示,实线为一简谐波该时刻的波形图,虚线是该波经0.2s后的波形图. 打一个点,每打5个点取一个计数点,A、B、C、D是四个计数点,纸带上C点对应的物体的瞬时速度为
打一个点,每打5个点取一个计数点,A、B、C、D是四个计数点,纸带上C点对应的物体的瞬时速度为  ,该物体的加速度为
,该物体的加速度为  。
。
 ”或“
”或“ ”)。
”)。