题目内容
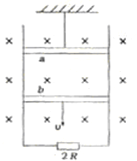 (2010?南昌二模)间距为L的平行光滑导轨固定在竖直平面同,磁感应强度为B,方向水平的匀强磁场与导轨平面垂直,二根水平导体棒a、b的质量均为m,电阻均为R,横跨在导轨上且与导轨接触良好,其中a棒中心用一细线悬挂,导轨的下端连接阻值为2R的电阻,如图所示.线能承受的最大拉力为1.5mg.开始二棒紧靠在一起,释放b棒,b棒在运动过程中,始终与导轨垂直,当b棒下落h高时,绳恰好拉断.(重力加速度为g)
(2010?南昌二模)间距为L的平行光滑导轨固定在竖直平面同,磁感应强度为B,方向水平的匀强磁场与导轨平面垂直,二根水平导体棒a、b的质量均为m,电阻均为R,横跨在导轨上且与导轨接触良好,其中a棒中心用一细线悬挂,导轨的下端连接阻值为2R的电阻,如图所示.线能承受的最大拉力为1.5mg.开始二棒紧靠在一起,释放b棒,b棒在运动过程中,始终与导轨垂直,当b棒下落h高时,绳恰好拉断.(重力加速度为g)(1)求线拉断时流过a棒的电流大小;
(2)求线拉断时b棒的速度;
(3)从b棒释放到线拉断所用时间.
分析:对a棒受力分析,根据平衡条件列方程求解;
对b棒,先由并联电路的电流规律求出b棒的电流,然后根据欧姆定律球b棒的感应电动势,然后根据法拉第电磁感应定律求棒的速度;
在b棒下落到线被拉断的过程中,设所经历的时间为t,根据动量定理和电量的计算公式计算时间t.
对b棒,先由并联电路的电流规律求出b棒的电流,然后根据欧姆定律球b棒的感应电动势,然后根据法拉第电磁感应定律求棒的速度;
在b棒下落到线被拉断的过程中,设所经历的时间为t,根据动量定理和电量的计算公式计算时间t.
解答:解:(1)对a棒,根据平衡条件,绳的拉力F=mg+Fa安
且Fa安=BIaL
解得Ia=
(2)b棒切割磁感线产生感应电动势,相当于电源,外电路相当于a棒电阻与2R并联:通过b棒的电流Ib=Ia+I2R
2R电阻与a棒并联,电压相等,电流之比与电阻之比成反比,故I2R=
Ia
则Ib=
Ia
a棒与2R并联后的总电阻为:
=
R
导体棒b切割磁感线产生的感应电动势:E=Ib(R+
R)=
IbR
且E=BLv
解得:v=
(3)在b棒下落到线被拉断的过程中,设所经历的时间为t,则
mgt-BI平均Lt=mv
且I平均t=q=
=
解得:t=
+
答:(1)线拉断时流过a棒的电流大小为
;
(2)线拉断时b棒的速度为
;
(3)从b棒释放到线拉断所用时间
+
.
且Fa安=BIaL
解得Ia=
| mg |
| 2BL |
(2)b棒切割磁感线产生感应电动势,相当于电源,外电路相当于a棒电阻与2R并联:通过b棒的电流Ib=Ia+I2R
2R电阻与a棒并联,电压相等,电流之比与电阻之比成反比,故I2R=
| 1 |
| 2 |
则Ib=
| 3 |
| 2 |
a棒与2R并联后的总电阻为:
| R?2R |
| R+2R |
| 2 |
| 3 |
导体棒b切割磁感线产生的感应电动势:E=Ib(R+
| 2 |
| 3 |
| 5 |
| 3 |
且E=BLv
解得:v=
| 5mgR |
| 4B2L2 |
(3)在b棒下落到线被拉断的过程中,设所经历的时间为t,则
mgt-BI平均Lt=mv
且I平均t=q=
| △φ |
| R总 |
| 3BLh |
| 5R |
解得:t=
| 5mgR |
| 4B2L2 |
| 3B2L2h |
| 5mgR |
答:(1)线拉断时流过a棒的电流大小为
| mg |
| 2BL |
(2)线拉断时b棒的速度为
| 5mgR |
| 4B2L2 |
(3)从b棒释放到线拉断所用时间
| 5mgR |
| 4B2L2 |
| 3B2L2h |
| 5mgR |
点评:本题将电磁感应与力学知识电路知识综合在一起考查,关键是正确分析导体棒的运动形式然后结合对应规律列方程求解.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 (2010?南昌二模)如图所示,在一真空区域中,AB、CD是圆O的两条直径,在A、B两点上各放置电荷量为+Q和-Q的点电荷,设C、D两点的电场强度分别为EC、ED,电势分别为?C、?D,下列说法正确的是( )
(2010?南昌二模)如图所示,在一真空区域中,AB、CD是圆O的两条直径,在A、B两点上各放置电荷量为+Q和-Q的点电荷,设C、D两点的电场强度分别为EC、ED,电势分别为?C、?D,下列说法正确的是( ) (2010?南昌二模)如图所示为氢原子的能级图,已知可见的光子能量范围为1.62eV-3.11eV那么对氢原子在能级跃迁过程中发射或吸收光子的特征认识正确的是( )
(2010?南昌二模)如图所示为氢原子的能级图,已知可见的光子能量范围为1.62eV-3.11eV那么对氢原子在能级跃迁过程中发射或吸收光子的特征认识正确的是( ) (2010?南昌二模)由两个圆筒组成的汽缸是导热的,二个大小不同的可在圆筒内自由滑动的活塞间有一轻杆相连接,二个活塞封闭着一定质量的气体.整个装置水平放置,如图所示.此时活塞处于静止状态.当外界温度下降(大气压不变)活塞稍作移动重新平衡后,下列说法正确的是( )
(2010?南昌二模)由两个圆筒组成的汽缸是导热的,二个大小不同的可在圆筒内自由滑动的活塞间有一轻杆相连接,二个活塞封闭着一定质量的气体.整个装置水平放置,如图所示.此时活塞处于静止状态.当外界温度下降(大气压不变)活塞稍作移动重新平衡后,下列说法正确的是( )