题目内容
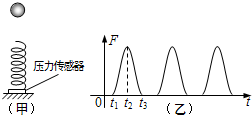如图（甲）所示，质量不计的弹簧竖直固定在水平面上，t=0时刻，将一金属小球从轻弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹起离开弹簧，上升到一定高度后再下落，如此反复．通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间t变化的图象如图（乙）如示，则
- A.小球加速度的最大值等于重力加速度g
- B.小球所受弹力的最大值等于其重力大小的2倍
- C.t2～t3这段时间内，小球增加的动能等于弹簧减少的弹性势能
- D.t2时刻，小球与弹簧组成的系统的势能出现最大值
D
分析：小球刚接触弹簧时加速度等于重力加速度，根据简谐运动对称性，分析小球运动到最低点时的加速度与重力加速度的关系，并根据牛顿第二定律分析小球所受弹力的最大值与重力的关系．t2～t3这段时间内，小球向上反弹，小球增加的动能和重力势能之和等于弹簧减少的弹性势能．t2时刻，小球运动到最低点，小球与弹簧组成的系统的势能出现最大值．
解答：
A、B，小球刚接触弹簧时，加速度等于重力加速度g，当小球运动到关于平衡位置对称点时，加速度大小等于g，但此时小球仍向下的速度，没有到达最低点，当小球运动到最低点时，弹簧的弹力增大，加速度将大于g，根据牛顿第二定律得知，小球所受弹力的最大值大于其重力大小的2倍．故AB错误．
C、t2～t3这段时间内，小球从最低点向上反弹，根据小球与弹簧组成的系统机械能守恒得知，小球增加的动能和重力势能之和等于弹簧减少的弹性势能．故C错误．
D、t2时刻，小球运动到最低点，动能为零，根据系统机械能守恒得到，小球与弹簧组成的系统的势能出现最大值．故D正确．
故选D
点评：本题运用牛顿运动定律和机械能守恒定律分析系统的加速度和能量变化．系统的能量有三种形式：动能、重力势能和弹性势能，总能量守恒．
分析：小球刚接触弹簧时加速度等于重力加速度，根据简谐运动对称性，分析小球运动到最低点时的加速度与重力加速度的关系，并根据牛顿第二定律分析小球所受弹力的最大值与重力的关系．t2～t3这段时间内，小球向上反弹，小球增加的动能和重力势能之和等于弹簧减少的弹性势能．t2时刻，小球运动到最低点，小球与弹簧组成的系统的势能出现最大值．
解答：
A、B，小球刚接触弹簧时，加速度等于重力加速度g，当小球运动到关于平衡位置对称点时，加速度大小等于g，但此时小球仍向下的速度，没有到达最低点，当小球运动到最低点时，弹簧的弹力增大，加速度将大于g，根据牛顿第二定律得知，小球所受弹力的最大值大于其重力大小的2倍．故AB错误．
C、t2～t3这段时间内，小球从最低点向上反弹，根据小球与弹簧组成的系统机械能守恒得知，小球增加的动能和重力势能之和等于弹簧减少的弹性势能．故C错误．
D、t2时刻，小球运动到最低点，动能为零，根据系统机械能守恒得到，小球与弹簧组成的系统的势能出现最大值．故D正确．
故选D
点评：本题运用牛顿运动定律和机械能守恒定律分析系统的加速度和能量变化．系统的能量有三种形式：动能、重力势能和弹性势能，总能量守恒．
练习册系列答案
相关题目
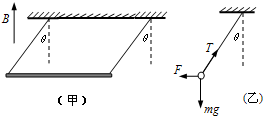如图（甲）所示，质量为m=50g，长l=10cm的铜棒，用长度也为l的两根轻软导线水平悬吊在竖直向上的匀强磁场中，磁感应强度B=1/3T．未通电时，轻线在竖直方向，通入恒定电流后，棒向外偏转的最大角度θ=37°，求此棒中恒定电流的大小．
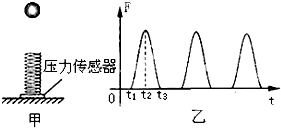如图（甲）所示，质量不计的弹簧竖直固定在水平面上，t=0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球落到弹簧上压缩弹簧到最低点，然后又被弹起离开弹簧，上升到一定高度后再下落，如此反复，通过安装在弹簧下端的压力传感器，测出这一过程弹簧弹力F随时间，变化的图象如图（乙）所示，则（ ）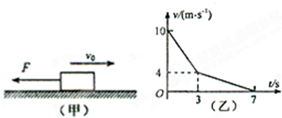
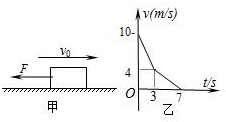如图（甲）所示，质量m=0.5kg，初速度υ0=10m/s的物体，受到一个与初速方向相反的外力F的作用，沿粗糙的水平面滑动，经3s撤去外力，直到物体停止，整个过程物体的υ-t图象如图（乙）所示，g取10m/s2，则下列判断正确的是（ ）
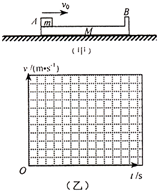如图（甲）所示，质量为M、长L=1.0m、右端带有竖直挡板的木板B，静止在光滑水平面上．质量为m的小木块（可视为质点）A，以水平速度v0=4.0m/s滑上B的左端，在右端与B碰撞后，最后恰好滑回木板B的左端．已知