题目内容
【题目】某种弹射装置的示意图如图所示,光滑的水平导轨MN右端N处于倾斜传送带理想连接,传送带长度L=15.0m,皮带以恒定速率v=5m/s顺时针转动,三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上,B、C之间有一段轻弹簧刚好处于原长,滑块B与轻弹簧连接,C未连接弹簧,B、C处于静止状态且离N点足够远,现让滑块A以初速度v0=6m/s沿B、C连线方向向B运动,A与B碰撞后粘合在一起.碰撞时间极短,滑块C脱离弹簧后滑上倾角θ=37°的传送带,并从顶端沿传送带方向滑出斜抛落至地面上,已知滑块C与传送带之间的动摩擦因数μ=0.8,重力加速度g=10m/s2 , sin37°=0.6,cos37°=0.8.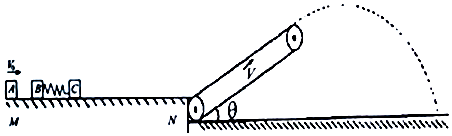
(1)滑块A、B碰撞时损失的机械能;
(2)滑块C在传送带上因摩擦产生的热量Q;
(3)若每次实验开始时滑块A的初速度v0大小不相同,要使滑块C滑离传送带后总能落至地面上的同一位置,则v0的取值范围是什么?(结果可用根号表示)
【答案】
(1)解:A与B位于光滑的水平面上,系统在水平方向的动量守恒,设A与B碰撞后共同速度为v1,选取向右为正方向,对A、B有:
mv0=2mv1…①
碰撞时损失机械能 ![]() …②
…②
解得△E=9J
答:滑块A、B碰撞时损失的机械能是9J;
(2)解:设A、B碰撞后,弹簧第一次恢复原长时AB的速度为vB,C的速度为vC.
由动量守恒:2mv1=2mvB+mvC…③
由机械能守恒: ![]() …④
…④
解得:vc=4m/s
C以vc滑上传送带,假设匀加速的直线运动位移为S时与传送带共速,由运动学公有:
式 ![]()
结合: ![]() ,
,
联立解得:x=11.25m<L
加速运动的时间为t,有: ![]() …⑤
…⑤
所以相对位移△x=vt﹣x
代入数据得:△x=1.25m…⑥
摩擦生热Q=umgcosθ△x=8J
答:滑块C在传送带上因摩擦产生的热量是8J;
(3)解:设A的最大速度为vmax,滑块C与弹簧分离时C的速度为vc1,AB的速度为vB1,则C在传送带上一直做加速度为a2的匀减速直线运动直到P点与传送带共速,有: ![]() …⑦
…⑦
加速度: ![]()
解得: ![]()
设A的最小速度为vmin,滑块C与弹簧分离时C的速度为vC2,AB的速度为vB1,则C在传送带上一直做加速度为a1的匀加速直线运动直到P点与传送带共速,有: ![]() …⑧
…⑧
解得: ![]() .
.
对A、B、C和弹簧组成的系统从AB碰撞后到弹簧第一次恢复原长的过程中,有:
mvmax=2mvB1+mcC1…⑨
机械能守恒: ![]() …⑩
…⑩
解得 ![]() ,
,
同理, ![]()
所以 ![]()
答:若每次实验开始时滑块A的初速度v0大小不相同,要使滑块C滑离传送带后总能落至地面上的同一位置,则v0的取值范围是 ![]() .
.
【解析】(1)A、B碰撞过程水平方向的动量守恒,由此求出二者的共同速度;由功能关系即可求出损失的机械能;(2)A、B碰撞后与C作用的过程中ABC组成的系统动量守恒,应用动量守恒定律与能量守恒定律可以求出C与AB分开后的速度,C在传送带上做匀加速直线运动,由牛顿第二定律求出加速度,然后应用匀变速直线运动规律求出C相对于传送带运动时的相对位移,由功能关系即可求出摩擦产生的热量.(3)应用动量守恒定律、能量守恒定律与运动学公式可以求出滑块A的最大速度和最小速度.

 阅读快车系列答案
阅读快车系列答案【题目】某实验小组正在测定一节新型电池的电动势(约为3V)和内阻,现要选取一个定值电阻R0当做保护电阻。
(1)首先为了准确测量定值电阻R0阻值,在操作台上准备了如下实验器材:
A.电压表V(量程3V,电阻约为4kΩ) |
B.电流表A1(量程1A,内阻约0.5Ω) |
C.电流表A2(量程3A,内阻约0.5Ω) |
D.定值电阻R0(阻值约为3Ω) |
E.滑动变阻器R(0-10Ω)
F.开关s一个,导线若干
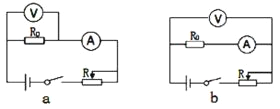
根据上述器材,在测量R0阻值时应选择________(填序号)为电流表,其实验电路图应选择以下哪种接法________(填字母a或b),经测量定值电阻R0阻值为2.8Ω。
(2)之后为了测量该新型电池的电动势和内阻,设计了如下实验,在下图中将所选 器材进行连接。
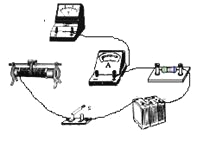
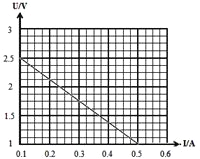
(3)根据实验记录做出U-I图线如图所示,从中可以求出待测新型电池的内阻为________Ω,电池电动势为________V(保留两位有效数字)。