题目内容
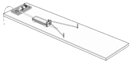
【题目】如图所示,物块A和B通过一根轻质不可伸长的细绳连接,跨放在质量不计的光滑定滑轮两侧,质量分别为mA=2kg、mB=1kg.初始时A静止于水平地面上,B悬于空中.先将B竖直向上再举高h=1.8m(未触及滑轮)然后由静止释放.一段时间后细绳绷直,A、B以大小相等的速度一起运动,之后B恰好可以和地面接触.取g=10m/s2 . 
(1)B从释放到细绳绷直时的运动时间t;
(2)A的最大速度v的大小;
(3)初始时B离地面的高度H.
【答案】
(1)解:B从释放到细绳刚绷直前做自由落体运动,有:h= ![]() gt2
gt2
代入数据解得:t=0.6 s.
答:运动时间为0.6s
(2)解:根据动量定理;
对A(取向上为正方向),则有:F2t﹣mAgt=mAv′,
对B,则有:﹣F1t+mBgt=mBv′﹣mBvB;
而F1=F2
且vB=6m/s,
得:﹣gt=2v′+v′﹣6
由于碰撞时间极短,因此有:v′=2 m/s
答:A的最大速度的大小为2m/s
(3)解:细绳绷直后,A、B一起运动,B恰好可以和地面接触,说明此时A、B的速度为零,
这一过程中A、B组成的系统机械能守恒,有:
![]() (mA+mB)v2+mBgH=mAgH
(mA+mB)v2+mBgH=mAgH
代入数据解得:H=0.6 m.
答:初始时B离地面的高度为0.6m
【解析】(1)根据自由落体规律计算运动时间;(2)根据动量守恒定律计算A的最大速度;(3)根据机械能守恒计算B离地面的高度H.

练习册系列答案
相关题目