Question

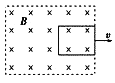
【题目】如图甲所示，一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m，NQ两端连接阻值R=3.0Ω的电阻，磁感应强度为B的匀强磁场垂直于导轨所在平面向上，导轨平面与水平面间的夹角为30°。一质量m=0.20kg，阻值r=1.0Ω的金属棒垂直于导轨放置并用不可伸长的绝缘细线通过光滑的定滑轮与质量M=0.80kg的重物相连。细线与金属导轨平行，金属棒由静止开始沿导轨向上滑行的速度V与时间t之间的关系如图乙所示，已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的，g=10m/s，求：

（1）0~0.3s内棒通过的位移。

（2）0~0.3s内绳子对金属棒做的功。

（3）电阻R在0~0.6s内产生的热量。

Answer 1

【答案】(1)0.4m (2)1.6J (3)3.75J

【解析】试题分析：（1）根据电量的表达式，结合法拉第电磁感应定律与闭合电路欧姆定律，从而导出电量的综合表达式，从而即可求解；（2）根据动能定理即可求解0~0.3s内绳子对金属棒做的功；（3）根据能量守恒定律，结合焦耳定律，从而即可求解．

（1）金属棒在0.3-0.6s内通过的电量是

金属棒在0-0.3s内通过的电量

由题：

代入解得：

（2）绳对重物做的功与绳对金属棒做的功大小相等

根据动能定理可得：

解得：

（3）金属棒在0-0.6S内通过的总位移为

代入数据解得x=1m

根据能量守恒定律

代入数据解得Q=5J

由于金属棒与电阻R串联，电流相等，根据焦耳定律得到它们产生的热量与电阻成正比

所以电阻R在0-0.6S内产生的热量为