题目内容
【题目】如图倾角为30°的直角三角形的底边BC长为2L , 处在水平位置,O为底边中点,直角边AB为光滑绝缘导轨,OD垂直AB。现在O处固定一带正电的物体,让一质量为m、带正电的小球从导轨顶端A静止开始滑下(始终不脱离导轨),测得它滑到D处受到的库仑力大小为F。则它滑到B处的速度大小为和加速度的大小 . (重力加速度为g)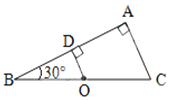
【答案】![]() ;
;![]() ?
?
【解析】由几何关系可得,D是AB线段的中点,OD是AB线段的中垂线,故BO=AO , 故AB在同一等势面上,所以,q由A到B的过程中电场中电场力作功为零;根据动能定理,有 ![]() ,解得
,解得 ![]() ;根据几何关系可得
;根据几何关系可得 ![]() ,设O点带电体的电荷量为Q , 则根据库仑定律可得:在D点的库仑力为
,设O点带电体的电荷量为Q , 则根据库仑定律可得:在D点的库仑力为 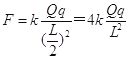 ,在B点,电荷q受重力、电场力和支持力,在平行AB杆的方向,在B点受的库仑力为
,在B点,电荷q受重力、电场力和支持力,在平行AB杆的方向,在B点受的库仑力为 ![]() ,方向水平向左,以AB轴和垂直AB方向建立坐标轴,根据正交分解可得:
,方向水平向左,以AB轴和垂直AB方向建立坐标轴,根据正交分解可得: ![]() ,解得
,解得 ![]() .
.
【考点精析】通过灵活运用库仑定律,掌握在真空中两个点电荷间的作用力跟它们的电荷量的乘积成正比,跟它们之间的距离的平方成反比,作用力的方向在它们的连线上;适用条件:真空中的点电荷即可以解答此题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目