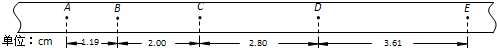题目内容
如图是一同学在研究匀变速直线运动时得到的一条纸带,相邻两计数点间的时间为T,下列能精确计算加速度a的方法中正确的有( )


A、测出AB和BD,用a=
| ||||||
B、测出AB和BD,用a=
| ||||||
C、测出AD,用a=
| ||||||
D、认为模糊中点是C点,测出AB和BC,用a=
|
分析:根据连续相等时间内的位移之差是一恒量求出加速度,或通过某段时间内的平均速度等于中间时刻的瞬时速度,结合速度时间公式求出加速度.
解答:解:A、测出AB和BD,BD段的平均速度等于C点的瞬时速度,则vC=
,AB段的平均速度等于AB段中间时刻的瞬时速度,则v=
,则加速度a=
.故A错误.
B、测出AB和BD,根据连续相等时间内的位移之差是一恒量,则有BD-2AB=3aT2,解得加速度a=
.故B正确.
C、因为A点的速度不为零,不能通过AD=
a(3T)2,求出a=
.故C错误.
D、模糊中点不一定是C点,不能认为模糊中点是C点.故D错误.
故选:B.
| BD |
| 2T |
| AB |
| T |
| ||||
|
B、测出AB和BD,根据连续相等时间内的位移之差是一恒量,则有BD-2AB=3aT2,解得加速度a=
| BD-2AB |
| 3T2 |
C、因为A点的速度不为零,不能通过AD=
| 1 |
| 2 |
| 2AD |
| 9T2 |
D、模糊中点不一定是C点,不能认为模糊中点是C点.故D错误.
故选:B.
点评:解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,掌握纸带的处理,会通过纸带求解瞬时速度和加速度.

练习册系列答案
相关题目