题目内容
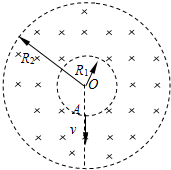 受控热核聚变装置中有极高的温度,因而带电粒子没有通常意义上的“容器”可装,而是由磁场约束带电粒子的运动使之束缚在某个区域内.现考虑这样一个实验装置:如图所示,在一个环状区域内有垂直于截面向里的匀强磁场,已知氘核的荷质比
受控热核聚变装置中有极高的温度,因而带电粒子没有通常意义上的“容器”可装,而是由磁场约束带电粒子的运动使之束缚在某个区域内.现考虑这样一个实验装置:如图所示,在一个环状区域内有垂直于截面向里的匀强磁场,已知氘核的荷质比| q | m |
分析:氦核从A点射出后,在磁感应强度为B的匀强磁场中做半径为r的匀速圆周运动,由洛仑兹力公式和牛顿第二定律求出半径r.
解答:解:作出氘核在磁场中运动而不穿出外边界的最大圆轨道如图中圆弧线所示,其圆心为O',半径为r
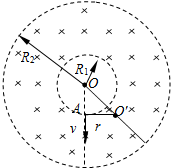
则有qvB=m
r=
=0.5m
两圆心间距离 OO'=
=0.707m
所以圆环区域的外径至少为
R2=OO′+r=1.207m
答:为了使该粒子不穿出磁场边界,则圆环的外半径R2至少应多大.

则有qvB=m
| v2 |
| r |
r=
| mv |
| qB |
两圆心间距离 OO'=
| R12+r2 |
所以圆环区域的外径至少为
R2=OO′+r=1.207m
答:为了使该粒子不穿出磁场边界,则圆环的外半径R2至少应多大.
点评:本题粒子在有圆形边界的磁场做匀速圆周运动的问题,画出轨迹,根据几何知识分析临界条件,求半径和圆心角是常用的思路.

练习册系列答案
相关题目
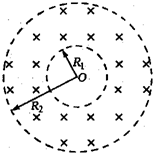
 据有关资料介绍,受控热核聚变装置中有极高的温度,因而带电粒子将没有通常意义上的“容器”可装,而是由磁场约束使其在某个区域内运动.现按下面的简化条件来讨论这个问题:如图所示是一个内径R1=1.0m,外径R2=2.0m的环状区域的截面,区域内有垂直截面向里的匀强磁场,O点为氦核源,它能沿半径方向射出各种速率的氦核,已知氦核的比荷
据有关资料介绍,受控热核聚变装置中有极高的温度,因而带电粒子将没有通常意义上的“容器”可装,而是由磁场约束使其在某个区域内运动.现按下面的简化条件来讨论这个问题:如图所示是一个内径R1=1.0m,外径R2=2.0m的环状区域的截面,区域内有垂直截面向里的匀强磁场,O点为氦核源,它能沿半径方向射出各种速率的氦核,已知氦核的比荷
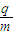 =4.8×107C/kg,不计氦核的重力和氢核间的相互作用,当射出的氦核最大速度为vm=1.44×107m/s时,求需要的约束磁场的磁感应强度至少为多少.
=4.8×107C/kg,不计氦核的重力和氢核间的相互作用,当射出的氦核最大速度为vm=1.44×107m/s时,求需要的约束磁场的磁感应强度至少为多少.