Question

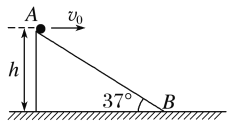
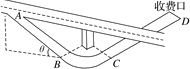
【题目】大爱无疆，最美逆行。一辆向武汉运输防疫物资的汽车经过高速公路的一个出口段，如图所示，车从出口A进入匝道，先匀减速直线通过下坡路段至B点（通过B点前后速率不变），再匀速率通过水平圆弧路段至C点，最后从C点沿平直路段匀减速到D点停下。已知车在A点的速度v0=90 km/h，AB长L1=100 m，与地面间的夹角θ=30°；BC为四分之一水平圆弧段，轮胎与BC段路面间的动摩擦因数为μ=0.5，最大静摩擦力可认为等于滑动摩擦力；CD段长L2=60 m。车在AB段所受阻力恒为车重的0.7倍，重力加速度g取10 m/s2。

(1)若汽车到达BC段时刚好达到BC段的限速vm（允许通过的最大速度），求vm；

(2)为保证行车安全，车轮不打滑，求水平圆弧段BC半径R的最小值；

(3)汽车从A点到D点全程的最短时间。

Answer 1

【答案】(1)15m/s；(2) 45m；(3)17.7s

【解析】

(1) 车在A点的速度

v0=90km/h=25m/s

AB长L1=100m，汽车在AB段做匀减速直线运动，有

0.7mg－mgsinθ=ma

vm2－v02=-2aL1

代入数据解得

vm=15m/s

(2)汽车在BC段做圆周运动，静摩擦力提供向心力，有

为了确保安全，则须满足

fm≤μmg

联立解得

R≥45m

即

Rmin=45m

(3)设通过AB段最短时间为t1，通过BC段最短时间为t2，通过CD段时间为t3，全程所用最短时间为t。有

L1=t1

πRmin=vmt2

L2=vmt3

t=t1＋t2＋t3

联立各式代入数据解得t=17.7s。