题目内容
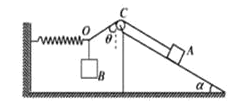
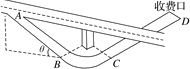
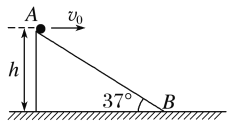
【题目】如图所示,倾角θ=37°的斜面位于水平地面上,小球从斜面顶端A点以初速度v0=4m/s水平向右抛出(此时斜面未动),小球恰好落到斜面底端B点处。空气阻力忽略不计,取重力加速度g=10 m/s2,tan 37°=0.75。
(1)求斜面的高度h;
(2)若在小球水平抛出的同时,使斜面以v=2 m/s开始向右做匀速直线运动,则小球经过多长时间落在斜面上?
【答案】(1)1.8m;(2)0.3s
【解析】
(1)小球水平抛出后恰好落在斜面底端,设水平位移为x,则
h=![]() gt2
gt2
x=v0t
由几何知识可得
tanθ=![]()
联立并代入已知数据得h=1.8m;
(2)如图所示:
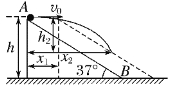
设经过时间t2小球落在斜面上,此时斜面运动的位移为x1,小球做平抛运动竖直位移为h2,水平位移为x2,则有:
x1=vt2
h2=![]() gt22
gt22
x2=v0t2
由几何知识可得
tanθ=![]()
联立解得
t2=0.3s

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目