题目内容
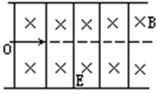
如图所示，在相互垂直的匀强磁场和匀强电场中放一光滑的足够长的斜面，倾斜角为30°，并固定在水平面上，电场强度为E，磁感应强度为B，质量为m，电量为+q的小球，静止在斜面的顶端，这时小球对斜面的正压力为零，若迅速地把电场方向改变为竖直向下，则小球能在斜面上滑多远？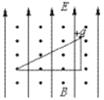
S=3m2g / 2q2B2
试题分析：电场向上时mg="qE" ，电场反向后重力与电场力的合力Ｆ=mg+qE=2mg
随速度增大洛仑兹力ｆ增大，当ｆ增大到与Ｆ垂直斜面的分力时，斜面支持力为零，小球将离开斜面。根据qvB=Fcos30°=2mgcos30°，可求出离开斜面时速度。设小球下滑距离为S，由动能定理有Fsin30°S=mv2/2，可解出S=3m2g / 2q2B2
点评：（1）对于带电粒子在复合场内运动问题首先要分清楚其运动特点和受力特点．
（2）要注意分析题目中的一些隐含条件，比如不计重力的带电粒子在正交的电场和磁场中直线运动时，一定是匀速直线运动；在混合场中做匀速圆周运动时，电场力与重力平衡．
（3）对于带电粒子在叠加场内的一般曲线运动问题（如类平抛），通常采用运动的合成与分解的方法来处理问题．还有就是要注意几何关系在解决物理问题中的应用．
练习册系列答案
阅读快车系列答案
相关题目
