题目内容
【题目】如图所示,匀强磁场的磁感应强度为B,方向垂直纸面向里,MN为其左边界.磁场中放置一半径为R的圆柱形金属圆筒,圆心O到MN的距离OO1=2R,金属圆筒轴线与磁场平行.金属圆筒用导线通过一个电阻r0接地,最初金属圆筒不带电.现有一电子枪对准金属圆桶中心O射出电子束,电子束从静止开始经过加速电场后垂直于左边界MN向右射入磁场区,已知电子质量为m,电量为e.电子重力忽略不计.求: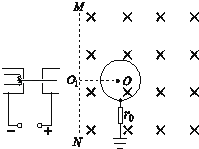
(1)最初金属圆筒不带电时,则
a.当加速电压为U时,电子进入磁场时的速度大小;
b.加速电压满足什么条件时,电子能够打到圆筒上;
(2)若电子束以初速度v0进入磁场,电子都能打到金属圆筒上(不会引起金属圆筒内原子能级跃迁),则当金属圆筒上电量达到相对稳定时,测量得到通过电阻r0的电流恒为I,忽略运动电子间的相互作用和金属筒的电阻,求此时金属圆筒的电势φ和金属圆筒的发热功率P.(取大地电势为零)
【答案】
(1)
解:a.设电子经过电场加速后的速度为v1,由动能定理,有:
![]()
解得:
![]()
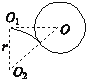
b.令电子恰好打在圆筒上时,加速电压为U0,设电子进入磁场时速度为v2,轨道半径为r,做出电子的轨迹如图所示,O2为轨道的圆心.
由几何关系得:
r2+(2R)2=(r+R)2
解得:
![]()
磁偏转过程,根据牛顿第二定律,有:
![]()
直线加速过程,根据动能定理,有:
![]()
解得:
![]()
所以当 ![]() 时,电子能够打到圆筒上.
时,电子能够打到圆筒上.
答:a.当加速电压为U时,电子进入磁场时的速度大小为 ![]() ;b.加速电压满足
;b.加速电压满足 ![]() 条件时,电子能够打到圆筒上;
条件时,电子能够打到圆筒上;
(2)
解:当圆筒上的电量达到相对稳定时,圆筒上的电荷不再增加,此时通过r0的电流方向向上.
根据欧姆定律,圆筒跟地面间的电压大小为:
U1=Ir0
由0﹣φ=U1可得:
φ=﹣Ir0
单位时间内到达圆筒的电子数:
![]()
故单位时间内到达圆筒上的电子的总能量:
![]()
单位时间内电阻消耗的能量:
![]()
所以圆筒的发热功率:
P=E﹣Er= ![]() ﹣I2r0
﹣I2r0
答:此时金属圆筒的电势φ为=Ir0,金属圆筒的发热功率P为 ![]() ﹣I2r0.
﹣I2r0.
【解析】本题第一问关键是明确电子的运动规律,画出电子运动的临界轨迹,然后根据牛顿第二定律、动能定理列式分析;第二问关键是根据能量守恒定律、焦耳定律列式求解.
【考点精析】关于本题考查的动能定理的综合应用和机械能综合应用,需要了解应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷;系统初态的总机械能E 1 等于末态的总机械能E 2 ,即E1 =E2;系统减少的总重力势能ΔE P减 等于系统增加的总动能ΔE K增 ,即ΔE P减 =ΔE K增;若系统只有A、

 阅读快车系列答案
阅读快车系列答案