Question

在一次抗洪抢险活动中，解放军某部动用直升飞机抢救落水人员，静止在空中的直升飞机上电动机通过悬绳将人从离飞机90m处的洪水中吊到机舱里．已知人的质量为80kg，吊绳的拉力不能超过1200N，电动机的最大输出功率为12kw，为尽快把人安全救起，操作人员采取的办法是：先让吊绳以最大拉力工作一段时间，而后电动机又以最大功率工作，当人到达机舱时恰好达到最大速度．（g=10m/s²）求：（1）人刚到达机舱时的速度；（2）这一过程所用的时间．

Answer 1

（1）15m/s（2）t= 5.75s．

解析试题分析：（1）吊绳先以最大的拉力工作，可知物体先做匀加速直线运动，当电动机达到最大功率，功率不变，速度增大，拉力减小，即物体做加速度减小的加速运动，当加速度减小到0，速度达到最大．所以拉力等于重力速度最大．
（2）全过程分两过程，第一阶段匀加速直线运动，根据匀变速运动求出时间，第二阶段加速度减小的加速运动，根据动能定理求出时间．
解：（1）第一阶段以最大拉力拉着物体匀加速上升，当电动机达到最大功率时，功率保持不变，物体变加速上升，速度增大，拉力减小，当拉力与重力相等时速度达到最大．此时有：P_m=mgv_m
代入数据解得，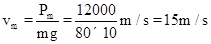
此速度也是物体到达机舱的速度．
故落水物体刚到达机舱时的速度为15m/s．
（2）对于第一段匀加速，加速度设为a，末速设为v₁，上升高度h₁，则有：
F_m-mg=ma
P_m=F_mv₁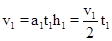
代入数据解得：v₁=10m/s，t₁=2s，h₁=10m
第二段，以最大功率上升，由动能定理得：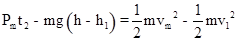 
解得t₂=5.75s
所以吊起落水物体所用总时间为t=t₁+t₂=7.75s
故这一过程所用的时间为7.75s．
考点：牛顿第二定律；功率、平均功率和瞬时功率；动能定理的应用．
点评：解决本题的关键分析出物体整个过程做什么运动，抓住先是恒定加速度运动，然后是恒定功率运动去分析．