题目内容
【题目】如图所示，竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成，AB恰与圆弧CD在C点相切，轨道固定在水平面上．一个质量为m的小物块（可视为质点）从轨道的A端以初动能E冲上水平轨道AB，沿着轨道运动，由DC弧滑下后停在水平轨道AB的中点．已知水平轨道AB长为L．求：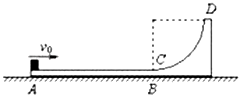
（1）小物块与水平轨道的动摩擦因数μ．
（2）为了保证小物块不从轨道的D端离开轨道，圆弧轨道的半径R至少是多大？
（3）若圆弧轨道的半径R取第（2）问计算出的最小值，增大小物块的初动能，使得小物块冲上轨道后可以达到最大高度是1.5R处，试求物块的初动能并分析物块能否停在水平轨道上．如果能，将停在何处？如果不能，将以多大速度离开水平轨道．
【答案】
（1）
解：小物块最终停在AB的中点，在这个过程中，由动能定理得：﹣μmg（L+0.5L）=﹣E
得：μ= 
（2）
解：若小物块刚好到达D处，速度为零，同理，有：﹣μmgL﹣mgR=﹣E
解得CD圆弧半径至少为：R= 
（3）
解：设物块以初动能E′冲上轨道，可以达到的最大高度是1.5R，由动能定理得：
﹣μmgL﹣1.5mgR=﹣E′
解得：E′= 
物块滑回C点时的动能为EC=1.5mgR= 
，由于EC＜μmgL= 
，故物块将停在轨道上．
设到A点的距离为x，有﹣μmg（L﹣x）=﹣EC
解得：x= 
L
即物块最终停在水平滑道AB上，距A点 L处
【解析】（1）在小物块运动的整个过程中，重力做功为0，摩擦力做负功﹣1.5μmgL，根据动能定理求解μ．（2）小物块恰好不从轨道的D端离开轨道时，到达D点速度为零，由动能定理求出R．（3）根据动能定理求解出小物块恰好冲上最大高度1.5R时的初动能E′，物块滑回C点时的动能EC=1.5mgR，分析EC与滑块从B到A克服摩擦力做功的大小关系，即可判断物块能否停在水平轨道上．并能根据动能定理求解滑块停止在轨道何处．
阅读快车系列答案
【题目】小张和小明测绘标有“3．8 V 0．4 A”小灯泡的伏安特性曲线，提供的实验器材有：
A．电源E（4 V，内阻约0．4 Ω） |
B．电压表V（2 V，内阻为2 kΩ） |
C．电流表A（0．6 A，内阻约0．3 Ω） |
D．滑动变阻器R（0～10Ω） |
E．三个定值电阻（R1=1kΩ，R2=2kΩ，R3=5kΩ）
F．开关及导线若干
（1）小明研究后发现，电压表的量程不能满足实验要求，为了完成测量，他将电压表进行了改装．在给定的定值电阻中选用 （选填“R1”、“R2”或“R3”）与电压表 （选填 “串联”或“并联”），完成改装．
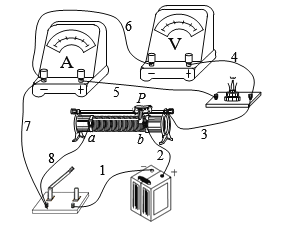
（2）小张选好器材后，按照该实验要求连接电路，如图所示（图中电压表已经过改装）．闭合开关前，小明发现电路中存在两处不恰当的地方，分别是：① ；② ．
（3）正确连接电路后，闭合开关，移动滑动变阻器的滑片P，电压表和电流表的示数改变，但均不能变为零．由此可以推断电路中发生的故障可能是导线 （选填图中表示导线的序号）出现了 （选填“短路”或“断路”）．
