Question

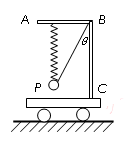
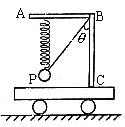
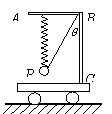
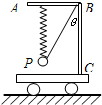如图所示，在动力小车上固定一直角硬杆ABC，分别系在水平直杆AB两端的轻弹簧和细线将小球P悬吊起来．轻弹簧的劲度系数为k，小球P的质量为m．
（1）当小车静止时，轻弹簧保持竖直，而细线与杆的竖直部分的夹角为α，试求此时弹簧的形变量和细线受到的拉力
（2）当小车沿水平地面以加速度a向右运动而达到稳定状态时，轻弹簧保持竖直，而细线与杆的竖直部分的夹角为θ，试求此时弹簧的形变量．

Answer 1

分析：（1）小车静止时，由于弹簧竖直，球受重力和弹簧的弹力，二力平衡，细线对小球没有作用力，可以用假设法，若细线对小球有拉力则弹簧不能竖直，故细线的拉力为零．由二力平衡可以求弹力，继而求形变量
（2）小球受重力，弹力，细线的拉力，由此可以列水平的牛顿第二定律方程和竖直的平衡方程，但是本题由于不知道重力，弹力，加速等的具体数值，因此对小球来说，其弹力①可能向上，②可能没有，③可能向下，由此需做三种讨论，以便确定弹簧形变量．

解答：解：
（1）小车静止时，由于弹簧竖直，球受重力和弹簧的弹力，二力平衡，细线对小球没有作用力，可以用假设法，若细线对小球有拉力则弹簧不能竖直，故细线的拉力为零．
对小球：
kx₁=mg
解得：
x₁=

mg

k

（2）小球受力如图：

水平方向有：
Tsinθ=ma
竖直方向有：
F+Tcosθ=mg
讨论：
①当Tcosθ=mg时，F等于0，故形变量x=0
②当Tcosθ＜mg，F向上
故有F+macotθ=mg
解得：
F=mg-macotθ
弹簧形变量为：
x=

F

k

=

mg-macotθ

k

③当Tcosθ＞mg，F向下
竖直方向有：F+mg=Tcosθ
解得：
F=Tcosθ-mg
=macotθ-mg
弹簧形变量为：
x=

F

k

=

macotθ-mg

k

答：
（1）弹簧的形变量为

mg

k

  细线的拉力为F=0
（2）弹簧形变量为：
①当Tcosθ=mg时，F等于0，故形变量x=0
②当Tcosθ＜mg，F向上，形变量为x=

mg-macotθ

k

③当Tcosθ＞mg，F向下，形变量为x=

macotθ-mg

k

点评：本题是弹簧类的题目中常规的一类，重点是对弹力的方向做讨论，以此才能确定形变量，题目难度不大，易错点在于忽略弹力方向的讨论．