题目内容
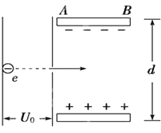
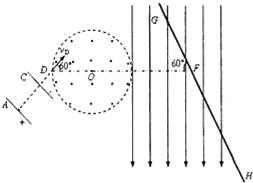
【题目】实验室常用电场和磁场来控制带电粒子的运动．在真空中A、C两板之间加上电压U，粒子被加速后从D点进入圆形有界磁场；匀强磁场区域以O为圆心，半径
，磁感应强度B方向垂直纸面向外；其右侧有一个足够大的匀强电场，方向竖直向下，左边界与圆形磁场边界相切；现在电场区域放置一块足够长档板GH，它与水平线FD夹角为60°（F点在档板上，圆心O位于在FD上），且OF=3R，如图所示．一比荷
的带正电粒子，从A板附近由静止释放，经U=150V电压加速后，从D点以与水平线成60°角射入磁场，离开圆形磁场时其速度方向与DF平行，最后恰好打在档板上的F点．不计粒子重力，求
（1）粒子进入磁场时的速度大小vD；
（2）磁感应强度B的大小；
（3）粒子到达F点时的速度大小vF；
（4）不改变其他条件，逐渐增大匀强电场的电场强度，要使粒子仍能打到挡板上，求所加电场场度的最大值．
【答案】（1）1×104m/s （2）0.1T （3）1.3×104m/s （4）1000V/m
【解析】试题分析：（1）对在加速电场中的加速过程根据动能定理列式求解速度；粒子在磁场中做匀速圆周运动，作出运动的轨迹，结合几何关系得到轨道半径，然后运用洛伦兹力等于向心力列式求解；粒子在偏转电场中做类似平抛运动，根据分运动公式列式求解末速度；临界条件是粒子打在极板上时速度方向与GH平行，结合分运动公式和几何关系列式分析即可。
（1）粒子在电压为U的加速电场中，由动能定理可得： 
代入数据解得： 
（2）根据题分析知，粒子在有界磁场中做圆周运动的圆心N恰好在圆周上，从M点水平射出磁场，设轨迹如图：
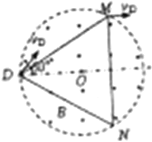
由此得到圆周运动半径为： 
根据洛伦兹力提供向心力： 
代入数据解得：B=0.1T
（3）粒子进入电场（MF）后做类似平抛运动，
在水平分位移： 
竖直分位移：y=Rsin60°=0.15m
又x=vDt，竖直方向： 
，合速度为： 
代入解得： 
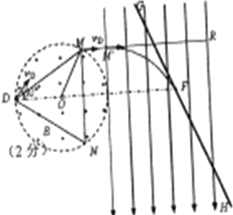
（4）当电场强度取到最大值E时，临界条件是粒子打到板上时轨道恰好与板面相切，即速度方向沿板GH，如图，
由类似平抛运动的规律，粒子的速度反向延长线交水平位移的中点Q，有MQ=QR
根据几何关系： 
根据
，vy=at，速度关系为：vy=vDtan60°，加速度为： 
联立解得：E=1000V/m
