题目内容
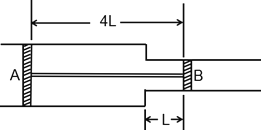
【题目】如图,竖直固定的倒U型导轨NNPQ,轨道间距L=0.8m,上端开小口与水平 线圈C连接,线圈面积S =0.8m2,匝数N- 200,电阻r=15Ω。质量m= 0.08kg的导体棒ab被外力水平压在导轨一侧,导体棒接入电路部分的电阻R=1Ω。开始时整个装 置处于竖直向上的匀强磁场中。r=0时撤去外力,同时磁感应强度按B=Bo-kt的规律变化,其中k= 0.4T/s;t1=ls时,导体棒开始F滑,它与导轨问的动摩擦因数μ = 0.5,设最大静摩擦力等于滑动摩擦力。其余电阻不计(重力加速度g= 10m/s2)。求:

(1) 0-1s内通过导体棒的电流强度;
(2) t=0时的磁感应强度B0;
(3)若仅将磁场方向改为竖直向下,要使导体棒ab在0- Is内仍静止,是否需要将它靠在导轨的另一侧?扼要说明理由。
【答案】(1) ![]() (2)
(2) ![]() (3)不需要
(3)不需要
【解析】
(1)根据法拉第电磁感应定律结合全电路的欧姆定律求解通过导体棒的电流强度;(2)分析导体棒在水平和竖直方向的受力情况,结合平衡方程求解B0;(3)用楞次定律说明理由。
(1)0-t1时间内,对线圈C和整个回路有:![]()
![]()
![]()
联立并带入数据解得I=4A
(2)t1=1s时刻,导体棒即将下滑,有:mg=Ff
Ff=μFN;
FN=B1IL
B1=B0-kt1
联立并代入数据解得B0=0.9T
(3)不需要;理由:由楞次定律可知,磁场方向相反,感应电流方向也相反,由左手定则可知导体棒所受安培力的方向不变,所以不需要将它靠在导轨的另一侧。

练习册系列答案
相关题目