题目内容
 (1)用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若测得各落点痕迹到O点的距离:OM=2.68cm,OP=8.62cm,ON=11.50cm,并知A、B两球的质量比为2:1,则未放B球时A球落地点是记录纸上的
(1)用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若测得各落点痕迹到O点的距离:OM=2.68cm,OP=8.62cm,ON=11.50cm,并知A、B两球的质量比为2:1,则未放B球时A球落地点是记录纸上的| |p-p′| |
| p |

(2)一多用电表的电阻档有三个倍率,分别是×1、×10、×100.用×10档测量某电阻时,操作步骤正确,发现表头指针偏转角度很小,为了较准确地进行测量,应换到
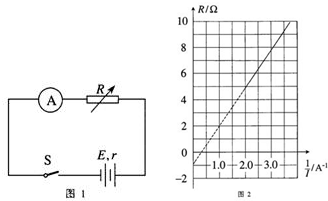
(3)某研究性学习小组利用图1所示电路测量电池组的电动势E和内阻r.根据实验数据绘出如图2所示的R-
| 1 |
| L |
分析:(1)A与B相撞后,B的速度增大,A的速度减小,都做平抛运动,竖直高度相同,所以水平方向,B在A的前面;
小球离开水平槽后做平抛运动,它们下落的高度相同,在空中的运动时间相同,由于小球在水平方向上做匀速直线运动,小球运动时间相同,因此小球的水平位移与小球的初速度成正比,计算时可以用小球的水平位移表示小球的初速度;根据题目所给实验数据,求出实验的百分误差.
(2)欧姆表指针偏角较小时,电阻较大,换成大挡测量,电阻的阻值等于表盘读数乘以倍率.
(3)根据闭合电路欧姆定律得出R与
的关系式,通过图线的斜率和截距求出电动势和内阻的大小.
小球离开水平槽后做平抛运动,它们下落的高度相同,在空中的运动时间相同,由于小球在水平方向上做匀速直线运动,小球运动时间相同,因此小球的水平位移与小球的初速度成正比,计算时可以用小球的水平位移表示小球的初速度;根据题目所给实验数据,求出实验的百分误差.
(2)欧姆表指针偏角较小时,电阻较大,换成大挡测量,电阻的阻值等于表盘读数乘以倍率.
(3)根据闭合电路欧姆定律得出R与
| 1 |
| I |
解答:解:(1)A与B相撞后,B的速度增大,A的速度减小,碰前碰后都做平抛运动,高度相同,落地时间相同,所以P点是没有碰时A球的落地点,N是碰后B的落地点,M是碰后A的落地点;
系统碰撞前总动量p与碰撞后总动量p′的百分误差
=
=
≈2%.
(2)操作步骤正确,发现表头指针偏转角度很小,知电阻较大,应换到×100档,换挡后需重新欧姆调零.电阻的阻值22×100=2.2×103Ω.
(3)根据闭合电路欧姆定律得,E=IR+Ir,则R=
-r,知纵轴截距的绝对值表示内阻的大小,所以r=0.9Ω,图线的斜率表示电动势,则E=
=2.9V.
故答案为:(1)P;2
(2)×100;调零(或重新调零);2.2×103(或2.2k)
(3)2.9;0.9
系统碰撞前总动量p与碰撞后总动量p′的百分误差
| |p-p′| |
| p |
| |||||||
| mAvA |
| |||||||||||||
2mB
|
(2)操作步骤正确,发现表头指针偏转角度很小,知电阻较大,应换到×100档,换挡后需重新欧姆调零.电阻的阻值22×100=2.2×103Ω.
(3)根据闭合电路欧姆定律得,E=IR+Ir,则R=
| E |
| I |
| 7.8+0.9 |
| 3 |
故答案为:(1)P;2
(2)×100;调零(或重新调零);2.2×103(或2.2k)
(3)2.9;0.9
点评:截距本题的关键知道欧姆表的使用方法以及注意事项,以及知道验证动量守恒定律和测量电动势和内阻的原理,会通过图象法求解电动势和内阻.

练习册系列答案
相关题目
 用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图所示,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若测得各落点痕迹到O的距离:
用半径相同的两小球A、B的碰撞验证动量守恒定律,实验装置示意如图所示,斜槽与水平槽圆滑连接.实验时先不放B球,使A球从斜槽上某一固定点C由静止滚下,落到位于水平地面的记录纸上留下痕迹.再把B球静置于水平槽前端边缘处,让A球仍从C处由静止滚下,A球和B球碰撞后分别落在记录纸上留下各自的痕迹.记录纸上的O点是重垂线所指的位置,若测得各落点痕迹到O的距离: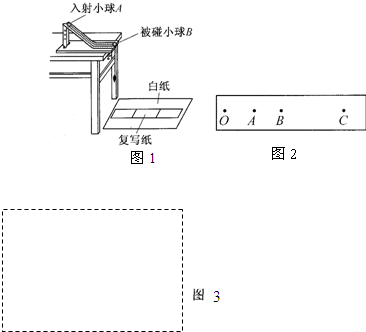




 = %(结果保留一位有效数字).
= %(结果保留一位有效数字). 图线,其中R为电阻箱读数,I为电流表读数,由此可以得到E= V,r= Ω.
图线,其中R为电阻箱读数,I为电流表读数,由此可以得到E= V,r= Ω.

