题目内容
如图所示，AB和CD是半径为R=1m的1／4圆弧形光滑轨道，BC为一段长2m的水平轨道质量为2kg的物体从轨道A端由静止释放，若物体与水平轨道BC间的动摩擦因数为0.1．求：
(1)物体第1次沿CD弧形轨道可上升的最大高度；
(2)物体最终停下来的位置与B点的距离。
(1)0.8m (2) B点的距离为2m
解析试题分析：：（1）设物体沿CD圆弧能上滑的最大高度为h，则此过程由动能定理可得：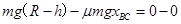
，解得
；
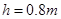（2）设物体在BC上滑动的总路程为s，则从下滑到静止的全过程由动能定理可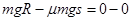得：
，解得
，即物体在BC上要来回滑动10m，一次来回滑动4m，故物体可完成2.5次的来回运动，最终停在C处，即离B点的距离为2m。
考点：考查了机械能守恒定律，动能定理
练习册系列答案
名校课堂系列答案
相关题目
质量为m的物体，从静止开始以3g/4的加速度竖直向下运动了h，以下判断中正确的是
| A．物体的机械能减少了mgh/4 |
| B．物体的动能增加了mgh/4 |
| C．物体的重力势能减少了3mgh/4 |
| D．物体的重力势能增加了mgh |
②0 ③
④
的有孔小球从杆上A点无初速下滑，已知q<<Q，AB=h，小球滑到B点时速度大小为
，则小球从A运动到B的过程中，电场力做的功为：______________；A、C两点间电势差为 ____________.
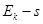图线如图所示。物体的初速度为______m/s，物体和水平面间的滑动摩擦因数为_______，拉力F的大小为_______N。（g取
）
水平速度弹射出去，沿水平直线轨道运动到B点后，进入半径R=0.3m的光滑竖直圆形轨道，运行一周后自B点向C点运动，C点右侧有一陷阱，C、D两点的竖直高度差h=0.2m，水平距离s=0.6m，水平轨道AB长为L1=1m，BC长为L2 =2.6m，小滑块与水平轨道间的动摩擦因数μ=0.5，重力加速度g=10m/s2。
