题目内容
4.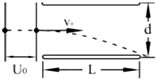 如图所示,一质子由静止经电压U0加速后,进入两块间距为d、电压为U的平行金属板之间,若质子从两板正中间垂直于电场方向射入,且刚好能从极板边缘穿出电场.试求:
如图所示,一质子由静止经电压U0加速后,进入两块间距为d、电压为U的平行金属板之间,若质子从两板正中间垂直于电场方向射入,且刚好能从极板边缘穿出电场.试求:(1)质子刚进入偏转电场的速度v0
(2)金属板的长度L
(3)质子穿出电场时的动能.
分析 (1)质子在加速电场中加速,应用动能定理可以求出质子的速度.
(2)质子进入偏转电场后做类平抛运动,沿水平方向做匀速直线运动,位移大小等于板长L;竖直方向做匀加速直线运动,位移大小等于板间距离的一半,由牛顿第二定律求出加速度,由运动学公式求解板长L.
(3)从刚开始到射出电场的过程中运用动能定理即可求出质子穿出电场时的动能.
解答 解:(1)质子在加速电场中,由动能定理得:eU0=$\frac{1}{2}$mv02-0,
解得:v0=$\sqrt{\frac{2e{U}_{0}}{m}}$;
(2)质子在偏转电场中做类平抛运动,
竖直方向:$\frac{d}{2}$=$\frac{1}{2}$$\frac{eU}{md}$t2,
水平方向:L=v0t,
解得:L=d$\sqrt{\frac{2{U}_{0}}{U}}$;
(3)在偏转电场中,由动能定理得:
e•$\frac{U}{d}$•$\frac{d}{2}$=EK-$\frac{1}{2}$mv02,
解得:EK=e(U0+$\frac{U}{2}$);
答:(1)质子刚进入偏转电场的速度V0为$\sqrt{\frac{2e{U}_{0}}{m}}$;
(2)金属板的长度L为d$\sqrt{\frac{2{U}_{0}}{U}}$;
(3)质子穿出电场时的动能为e(U0+$\frac{U}{2}$).
点评 本题是组合场问题,关键是分析质子的分析情况和运动情况.在偏转电场中质子做类平抛运动,采用运动的分解方法研究.

练习册系列答案
相关题目
14.如图,有一轮绕固定轴O转动,对于轮上的A、B两点,说法正确的是( )


| A. | 角速度相同 | B. | 线速度相同 | ||
| C. | 周期相同 | D. | 到轴心的距离相同 |
15.如图为电场中的一条电场线,其中a、b、c、d四点中ab=cd,下列的判断正确的是( )

| A. | a点场强一定大于c点的场强 | |
| B. | Uab一定为正值 | |
| C. | Uab一定等于Ucd | |
| D. | 若a点处的正电荷只在电场力作用下,一定沿电场线方向移动 |
12.如图是甲、乙两物体做直线运动的s-t图象,由图可知( )


| A. | t0~t1时间内,甲的速度比乙的速度小 | |
| B. | t0~t1时间内,甲的速度比乙的速度大 | |
| C. | t1时刻,两物体的速度大小相等 | |
| D. | 0~t1时间内,甲的位移比乙小 |
19.某电解电容器上标有“25V、470μF”的字样,对此,下列说法正确的是( )
| A. | 此电容器在直流25V及以下电压正常工作 | |
| B. | 25V是该电容器的击穿电压 | |
| C. | 当工作电压是25V时,电容才是470μF | |
| D. | 电容器没有充电时,电容为0 |
9.中国载人航天取得举世瞩目的成绩,在不久的将来中国人将登上月球.设想中国某宇航员在月球表面附近做简单实验,以初速度v0竖直向上抛出一个小球,经时间t后回到出发点.已知月球的半径为R.万有引力常量为G.则下列说法正确的是( )
| A. | 月球表面的重力加速度大小为$\frac{{v}_{0}}{t}$ | |
| B. | 月球的质量为$\frac{2{v}_{0}{R}^{2}}{Gt}$ | |
| C. | 绕月球做匀速圆周运动的卫星的最大运行速度大小为$\sqrt{\frac{{v}_{0}R}{t}}$ | |
| D. | 绕月球做匀速圆周运动的卫星的周期为$\sqrt{\frac{2Rt}{{v}_{0}}}$ |
16.长为L的细线一端系一质量为m的小球(可视为质点),另一端固定在一光滑锥顶上,光滑锥顶角为2θ,轴线在竖直方向,如图1所示.使小球在水平面内做角速度为ω的匀速圆周运动,线的张力为T,经分析可得T-ω2的关系图象如图2所示,已知重力加速度为g.则( )


| A. | a=mgsin θ | B. | b=$\frac{g}{L}$ | ||
| C. | 图线1的斜率k1=mLsin θ | D. | 图线2的斜率k2=ML |
14.荡秋千是一种常见的娱乐休闲活动,也是我国民族运动会的一个比赛项目.小娟同学荡秋千时,在从一侧的最高点荡到另一侧的最高点这一过程中,小娟的( )
| A. | 重力势能一直减小 | B. | 动能一直增大 | ||
| C. | 动能先减小后增大 | D. | 重力势能先减小后增 |
