题目内容
如下图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4 m的![]() 圆管轨道,已知AB圆管轨道半径与“0”字型圆形轨道半径相同.“9”管道是由半径为2R的光滑
圆管轨道,已知AB圆管轨道半径与“0”字型圆形轨道半径相同.“9”管道是由半径为2R的光滑![]() 圆弧和半径为R的光滑
圆弧和半径为R的光滑![]() 圆弧以及两段光滑的水平管道、一段光滑的竖直管道组成,“200”管道和“9”管道两者间有一小缝隙P,现让质量m=0.5 kg的闪光小球(可视为质点)从距A点高H=2.4 m处自由下落,并由A点进入轨道AB,已知小球到达缝隙P时的速率为v=8 m/s,g取10 m/s2.求:
圆弧以及两段光滑的水平管道、一段光滑的竖直管道组成,“200”管道和“9”管道两者间有一小缝隙P,现让质量m=0.5 kg的闪光小球(可视为质点)从距A点高H=2.4 m处自由下落,并由A点进入轨道AB,已知小球到达缝隙P时的速率为v=8 m/s,g取10 m/s2.求:
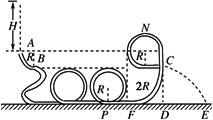
(1)小球通过粗糙管道过程中克服摩擦阻力做的功;
(2)小球通过“9”管道的最高点N时对轨道的作用力;(3)小球从C点离开“9”管道之后做平抛运动的水平位移以及小球落地时速度的大小.
解析:
|
答案:(1)2 J (2)35 N (3)8 m/s 2.77 m 解析:(1)小球从初始位置到达缝隙P的过程中,由动能定理有 mg(H+3R)-WF= 代入数据得WF=2 J. (2)设小球到达最高点N时的速度为vN,由机械能守恒定律有 在最高点N时,根据牛顿第二定律有FN+mg= 联立解得FN= 所以小球在最高点N时对轨道的作用力为35 N. (3)小球从初始位置到达C点的过程中,由动能定理有 mg(H+R)-WF= 解得vC=6.93 m/s 小球从C点离开“9”管道之后做平抛运动, 竖直方向:2R= 水平方向:DE=vCt=2.77 m 所以平抛运动的水平位移为2.77 m 落地时速度的大小为vE= |

 如图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的
如图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的

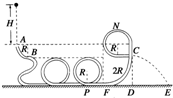 如图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的
如图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的 圆管轨道,已知AB圆管轨道半径与“0”字型圆形轨道半径相同.“9”管道是由半径为2R的光滑
圆管轨道,已知AB圆管轨道半径与“0”字型圆形轨道半径相同.“9”管道是由半径为2R的光滑 圆弧和半径为R的光滑
圆弧和半径为R的光滑 圆弧以及两段光滑的水平管道、一段光滑的竖直管道组成,“200”管道和“9”管道两者间有一小缝隙P,现让质量m=0.5kg的闪光小球(可视为质点)从距A点高H=2.4m处自由下落,并由A点进入轨道AB,已知小球到达缝隙P时的速率为v=8m/s,g取10m/s2.求:
圆弧以及两段光滑的水平管道、一段光滑的竖直管道组成,“200”管道和“9”管道两者间有一小缝隙P,现让质量m=0.5kg的闪光小球(可视为质点)从距A点高H=2.4m处自由下落,并由A点进入轨道AB,已知小球到达缝隙P时的速率为v=8m/s,g取10m/s2.求: