题目内容
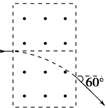 如图所示,在一矩形区域内,不加磁场时,不计重力的带电粒子以某一初速度垂直左边界射入,穿过此区域的时间为t.若加上磁感应强度为B水平向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出时偏离原方向60°,求带电粒子的比荷.
如图所示,在一矩形区域内,不加磁场时,不计重力的带电粒子以某一初速度垂直左边界射入,穿过此区域的时间为t.若加上磁感应强度为B水平向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子飞出时偏离原方向60°,求带电粒子的比荷.分析:不加磁场时粒子做匀速直线运动;加入磁场后,带电粒子在磁场中做圆周运动,已知偏向角则由几何关系可确定圆弧所对应的圆心角,则可求得圆的半径,由洛仑兹力充当向心力可求得带电粒子的比荷.
解答:解:由带电粒子在磁场中运动的偏向角,可知带电粒子运动轨迹所对的圆心角为60°,因此由几何关系l=Rsin 60°;
由Bqv0=m
得R=
故l=
sin 60°,
又未加磁场时有l=v0t,所以可求得
比荷
=
.
由Bqv0=m
| v02 |
| R |
得R=
| mv0 |
| qB |
故l=
| mv0 |
| qB |
又未加磁场时有l=v0t,所以可求得
比荷
| q |
| m |
| sin60° |
| Bt |
点评:带电粒子在磁场中的运动类题目关键在于确定圆心和半径,然后由向心力公式即可确定半径公式,由几何关系即可求解.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 如图所示,在纸平面内建立的直角坐标系xoy,在第一象限的区域存在沿y轴正方向的匀强电场.现有一质量为m,电量为e的电子从第一象限的某点P(L,
如图所示,在纸平面内建立的直角坐标系xoy,在第一象限的区域存在沿y轴正方向的匀强电场.现有一质量为m,电量为e的电子从第一象限的某点P(L,
 ,ad与ac夹角为
,ad与ac夹角为 =300。一质量为
=300。一质量为 带电量为
带电量为 的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场,随后粒子经过ac与bd交点o进入Ⅱ区(粒子重力不计)。
的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场,随后粒子经过ac与bd交点o进入Ⅱ区(粒子重力不计)。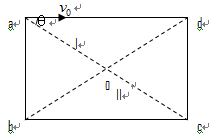
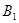 的方向和大小
的方向和大小 应满足的条件
应满足的条件 ,ad与ac夹角为
,ad与ac夹角为 =300。一质量为
=300。一质量为 带电量为
带电量为 的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场,随后粒子经过ac与bd交点o进入Ⅱ区(粒子重力不计)。
的粒子以速度V0从Ⅰ区边缘a点沿ad方向射入磁场,随后粒子经过ac与bd交点o进入Ⅱ区(粒子重力不计)。
 的方向和大小
的方向和大小 应满足的条件
应满足的条件