题目内容
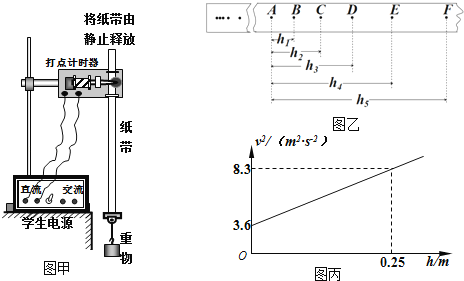
【题目】如图甲所示,轻弹簧竖直固定在水平面上,一质量为m = 0.2 kg的小球从弹簧上端某高度处自由下落,从它接触弹簧到弹簧压缩至最短的过程中(弹簧始终在弹性限度内),其速度v和弹簧压缩量x的函数图象如图乙所示,其中A为曲线的最高点,小球和弹簧接触瞬间的机械能损失不计,取重力加速度g = 10 m/s2,则下列说法中正确的是( )

A. 该弹簧的劲度系数为20 N/m
B. 当x = 0.3 m时,小球处于超重状态
C. 从接触弹簧到压缩至最短的过程中,小球的加速度先减小后增大
D. 小球刚接触弹簧时速度最大
【答案】ABC
【解析】
由图象可知,当△x=0.1m时,小球的速度最大,加速度为零,此时重力等于弹簧对它的弹力,根据k△x=mg求出k,再求出最低点的弹力,根据牛顿第二定律求解在最低点的加速度,与刚开始接触时比较得出什么时候加速度最大,小球和弹簧组成的系统机械能守恒。
由小球的速度图象知,开始小球的速度增大,说明小球的重力大于弹簧对它的弹力,当△x为0.1m时,小球的速度最大,然后减小,说明当△x为0.1m时,小球的重力等于弹簧对它的弹力。所以可得:k△x=mg,解得:![]() ,故A正确;当△x=0.3m时,物体的速度减小,加速度向上,故说明物体处于超重状态,故B正确;图中的斜率表示加速度,则由图可知,从接触弹簧到压缩至最短的过程中,小球的加速度先减小后增大,故C正确;由小球的速度图象知,开始小球的速度增大,小球的重力大于弹簧对它的弹力,当△x为0.1m时,小球的速度最大,然后速度减小,故D错误;故选ABC。
,故A正确;当△x=0.3m时,物体的速度减小,加速度向上,故说明物体处于超重状态,故B正确;图中的斜率表示加速度,则由图可知,从接触弹簧到压缩至最短的过程中,小球的加速度先减小后增大,故C正确;由小球的速度图象知,开始小球的速度增大,小球的重力大于弹簧对它的弹力,当△x为0.1m时,小球的速度最大,然后速度减小,故D错误;故选ABC。

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目