题目内容
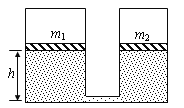
【题目】如图所示，两个可导热的气缸竖直放置，它们的底部由一细管连通（忽略细管的容积）。两气缸各有一个活塞，质量分别为m1和m2，活塞与气缸无摩擦。活塞的下方为理想气体，上方为真空。当气体处于平衡状态时，两活塞位于同一高度h.（已知m1＝2m，m2＝m）
（1）在两活塞上同时各放一质量为m的物块，求气体再次达到平衡后两活塞的高度差（假定环境温度始终保持为T0）；
（2）在达到上一问的终态后，环境温度由T0缓慢上升到1.25T0，试问在这个过程中，气体对活塞做了多少功？（假定在气体状态变化过程中，两物块均不会碰到气缸顶部）。
【答案】（1）x=h（2）0.75mgh
【解析】试题分析：（1）开始时两缸内的气压相等，从而可得出两活塞的面积关系，两活塞上同时各加一质量为m的物块后，就打破了原有的平衡，面积小的活塞会下沉，直至面积小的活塞移到底部，再确定左侧气体的状态参量，整个过程是等温变化，由气体的状态方程可得出左缸气体的高度，即为两活塞的高度差．（2）缓慢升温气体发生等压变化，根据盖吕萨克定律求体积变化，求出活塞移动的距离，根据W=Fl求功
（1）设左、右活塞的面积分别为S'和S，由于气体处于平衡状态，故两活塞对气体的压强相等，即： 
，由此得
在两个活塞上各加质量为m的物块后，假设左右两活塞仍没有碰到汽缸底部，
由平衡条件：P左=
，P右=
，P左＜P右，
则右活塞降至气缸底部，所有气体都在左气缸中。
在初态，气体的压强为
，体积为3Sh；在末态，气体压强为
，体积为2xS（x为左活塞的高度）
由玻意耳定律得： 
·3Sh=
·2xS解得：x=h，即两活塞的高度差为x=h
（2）当温度由T0上升至T=1.25T0时，气体的压强不变，设x'是温度达到T时左活塞的高度，
由盖·吕萨克定律得：x'=
x=1.25h活塞对气体做的功为：W= 
=3mg(x'－x)=0.75mgh
