题目内容
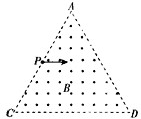如图所示，在边长为L的等边三角形ACD区域内，存在磁感应强度为B、方向垂直纸面向外的匀强磁场．现有一束质量为m、电荷量为+q的带电粒子，从AC边中点P、平行于CD边垂直磁场射入，粒子的重力可忽略不计．（1）若粒子进入磁场时的速度大小为v0，求粒子在磁场中运动的轨道半径；
（2）为使粒子能从CD边飞出磁场，粒子进入磁场时的速度大小应满足什么条件？
分析：（1）根据牛顿第二定律，由洛伦兹力提供向心力，则即可求解；
（2）粒子恰从CD边出磁场，根据几何关系，则可确定各自运动的半径．从而求出对应的速度，确定结果．
（2）粒子恰从CD边出磁场，根据几何关系，则可确定各自运动的半径．从而求出对应的速度，确定结果．
解答：解：（1）设粒子在磁场中运动的轨道半径为r，则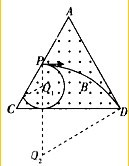
qv0B=m
解得：r=
（2）设粒子从CD边飞出磁场的最小半径为r1，对应最小速度为v1，则
r1=
sin60°=
qv1B=m
解得：v1=
设粒子能从D点飞出磁场，对应的半径为r2，速度为v2，圆心角为α，则
r
=（L-
）2+（r2-
）2
sinα=
解得：r2=
α=60°
由几何关系可知，粒子能从D点飞出磁场，且飞出时速度方向沿AD方向
由于qv2B=m
解得：v2=
所以速度大小应满足的条件：
＜v＜
答：（1）若粒子进入磁场时的速度大小为v0，粒子在磁场中运动的轨道半径为
；
（2）为使粒子能从CD边飞出磁场，粒子进入磁场时的速度大小应满足的条件为
＜v＜
．
qv0B=m
| ||
| r |
解得：r=
| mv0 |
| qB |
（2）设粒子从CD边飞出磁场的最小半径为r1，对应最小速度为v1，则
r1=
| L |
| 4 |
| ||
| 8 |
qv1B=m
| ||
| r1 |
解得：v1=
| ||
| 8m |
设粒子能从D点飞出磁场，对应的半径为r2，速度为v2，圆心角为α，则
r
2 2 |
| L |
| 4 |
| ||
| 4 |
sinα=
| 3L |
| 4r2 |
解得：r2=
| ||
| 2 |
由几何关系可知，粒子能从D点飞出磁场，且飞出时速度方向沿AD方向
由于qv2B=m
| ||
| r2 |
解得：v2=
| ||
| 2m |
所以速度大小应满足的条件：
| ||
| 8m |
| ||
| 2m |
答：（1）若粒子进入磁场时的速度大小为v0，粒子在磁场中运动的轨道半径为
| mv0 |
| qB |
（2）为使粒子能从CD边飞出磁场，粒子进入磁场时的速度大小应满足的条件为
| ||
| 8m |
| ||
| 2m |
点评：解决本题的关键是正确的确定从CD边射出的两个临界点，最右边是从D射出，但最左边不是从C射出，而是与下边界相切为临界．
练习册系列答案
相关题目
（2008?普陀区三模）如图所示，在边长为L的正方形ABCD区域内存在着场强为E的匀强电场，电场方向与AB边平行．一带电量为q的带电粒子以mv2/2从正方形ABCD一条边的中点射入（该粒子的重力不计），一段时间后，该粒子从一条边的中点射出，此时该带电粒子的动能有n种情况，则n 等于（ ）
（A）如图所示，在边长为L=1m的等边三角形ACD区域内，存在磁感应强度为B=
如图所示，在边长为l的正方形区域内，有与y轴平行的匀强电场和垂直于纸面的匀强磁场．一个带电粒子（不计重力）从原点O沿x轴进入场区，恰好做匀速直线运动，穿过场区的时间为T0；若撤去磁场，只保留电场，其他条件不变，该带电粒子穿过场区的时间为
如图所示，在边长为l的正方形四个顶点A、B、C、D上依次放置电荷量为+q、+q、+q和-q的点电荷，求正方形中心O点的电场强度．