题目内容
16.质量为0.04千克的质点作简谐振动,其运动方程为x=0.5cos(5t-$\frac{π}{2}$)米,式中t以秒计.求:(1)初始位移、初始速度;
(2)t=$\frac{4π}{3}$秒时的位移、速度和加速度;
(3)质点的位移大小为振幅的一半处且向x轴正向运动的时刻的速度、加速度和所受的力.
分析 (1)简谐运动的表达式为x=Asin(ωt+φ),A为振幅,ω为圆频率.将时间t=0代入即可求出初位移,求导即可求出初速度;
(2)将时间t=$\frac{4π}{3}$秒代入公式即可求出位移,求导即可求出速度,再次求导求出加速度;
(3)根据位移,求出对应的时间,然后同(2)的方法即可求出.
解答 解:(1)根据简谐振动的运动方程为x=0.5cos(5t-$\frac{π}{2}$)米,可知,t=0时刻:${x}_{0}=0.5•cos\frac{π}{2}=0$;对运动方程求导得:v=x′=-5×0.5sin(5t-$\frac{π}{2}$);当t=0时,v=2.5m/s.
(2)根据简谐振动的运动方程为x=0.5cos(5t-$\frac{π}{2}$)米,可知,t=$\frac{4π}{3}$时刻:${x}_{1}=0.5•cos(5×\frac{4π}{3}-\frac{π}{2})=0.5cos\frac{37π}{6}=\frac{\sqrt{3}}{4}$m;
对运动方程求导得:v=x′=-5×0.5sin(5t-$\frac{π}{2}$);当t=$\frac{4π}{3}$时,v1=-5×0.5sin(5×$\frac{4π}{3}$-$\frac{π}{2}$)=-1.25m/s.
对速度方程求导得:a=v′=x″=-12.5cos(5t-$\frac{π}{2}$);当t=$\frac{4π}{3}$时,a1=-12.5cos(5×$\frac{4π}{3}$-$\frac{π}{2}$)=$-\frac{25\sqrt{3}}{4}$m/s2
(3)在简谐振动的过程中当质点位移大小为振幅的一半处且向x轴正向运动的时刻,质点的位移可能为正,是0.25m,也可能为负是-0.25m:
①当x=0.25m时,在一个周期内,$(5t-\frac{π}{2})=\frac{5}{3}π$,质点的速度:v2=-2.5sin$\frac{5}{3}π$=$\frac{5\sqrt{3}}{4}$m/s,加速度:a2=-12.5cos$\frac{5}{3}π$=-6.25m/s2
质点所受的力:F1=ma2=0.04×(-6.25)=-0.25N
②当x=-0.25m时,在一个周期内,$(5t-\frac{π}{2})=\frac{4}{3}π$,质点的速度:v3=-2.5sin$\frac{4}{3}π$=$\frac{5\sqrt{3}}{4}$m/s,加速度:a3=-12.5cos$\frac{4}{3}π$=6.25m/s2
所受的力:F2=ma3=0.04×6.25=0.25N
答:(1)初始位移是0,初始速度是2.5m/s;
(2)t=$\frac{4π}{3}$秒时的位移是$\frac{\sqrt{3}}{4}$m,速度是-1.25m/s,加速度是$-\frac{25\sqrt{3}}{4}$m/s2;
(3)质点的位移大小为振幅的一半处且向x轴正向运动的时刻,①当x=0.25m时,质点的速度是$\frac{5\sqrt{3}}{4}$m/s,加速度是-6.25m/s2质点所受的力是-0.25N;②当x=-0.25m时,质点的速度是$\frac{5\sqrt{3}}{4}$m/s,加速度是6.25m/s2 所受的力 0.25N.
点评 解决本题的关键掌握简谐运动的表达式为x=Asin(ωt+φ),知道A为振幅,ω为圆频率.利用位移与速度、加速度的导数关系即可解决.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 点电荷是实际带电体的抽象,是一种理想化模型 | |
| B. | 点电荷自身不一定很小,所带的电荷不一定很少 | |
| C. | 体积大的物体,只要满足一定的条件,也可以看成点电荷 | |
| D. | 体积小于1mm3的带电体就是点电荷 |
 如图所示,用两支相同的弹簧秤吊着一根铜棒,铜棒所在的虚线框范围内有垂直纸面的匀强磁场,棒中通入自左向右的电流.当棒静止时,两弹簧秤示数均为F1;若将棒中电流反向而保持大小不变,当棒静止时,两弹簧秤的示数均为F2,且F2>F1,根据上面所给的信息,能求出( )
如图所示,用两支相同的弹簧秤吊着一根铜棒,铜棒所在的虚线框范围内有垂直纸面的匀强磁场,棒中通入自左向右的电流.当棒静止时,两弹簧秤示数均为F1;若将棒中电流反向而保持大小不变,当棒静止时,两弹簧秤的示数均为F2,且F2>F1,根据上面所给的信息,能求出( ) 如图所示,磁流体发电机的极板相距d=0.2m,极板间有垂直于纸面向里的匀强磁场,B=1.0T.外电路中可变负载电阻R用导线与极板相连.电离气体以速率v=1100m/s沿极板射入,极板间电离气体等效内阻r=0.1Ω,试求此发电机的电动势及最大输出功率.
如图所示,磁流体发电机的极板相距d=0.2m,极板间有垂直于纸面向里的匀强磁场,B=1.0T.外电路中可变负载电阻R用导线与极板相连.电离气体以速率v=1100m/s沿极板射入,极板间电离气体等效内阻r=0.1Ω,试求此发电机的电动势及最大输出功率.
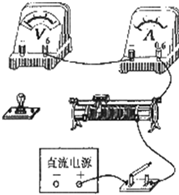 在描绘小灯泡伏安特性曲线的实验中,提供的实验器材有:
在描绘小灯泡伏安特性曲线的实验中,提供的实验器材有: