��Ŀ����
����Ŀ����ͼ��ʾ������ ![]() �⻬Բ����С��A�İ뾶ΪR����ֹ�ڹ⻬ˮƽ���ϣ�����C����ľ��B���Ҷˣ�A��B��C��������Ϊm��A��B��������ͬ����B��C����ͬ���ٶ����������˶���B��A����ճ����һ��Cǡ������A��Բ�����������Բ�ĵȸߴ�����
�⻬Բ����С��A�İ뾶ΪR����ֹ�ڹ⻬ˮƽ���ϣ�����C����ľ��B���Ҷˣ�A��B��C��������Ϊm��A��B��������ͬ����B��C����ͬ���ٶ����������˶���B��A����ճ����һ��Cǡ������A��Բ�����������Բ�ĵȸߴ�����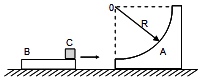
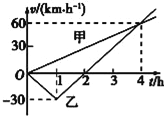
��1��B��Cһ�������˶����ٶ�Ϊ����
��2������C���ص�A�ĵ�ʱAB�����C���ٶ�Ϊ����
��3������C���ص�A�ĵ�ʱC��A��ѹ��Ϊ���٣�
���𰸡�
��1���⣺��BC�ij��ٶ�Ϊv0��AB���������ж����غ㣬������������2m���ٶ�u��ѡȡ��ҪΪ��������
mv0=2mu��
��u= ![]() v0��
v0��
C������ߵ�Ĺ����У��ɶ����غ㶨�ɣ�mv0+2m u=��m+2m��u��
�ɻ�е���غ㣺 ![]() mv02+
mv02+ ![]() 2mu2��
2mu2�� ![]() ��m+2m��u/2=mgh
��m+2m��u/2=mgh
��ã� ![]()
��B��Cһ�������˶����ٶ�Ϊ ![]() ��
��
��2���⣺C�ӵ˻��������ٴӶ��˻����ײ��Ĺ����У�����ˮƽ�������غ㡢��е���غ㣬�У�
mv0+2mu=mv1+2mv2
![]() mv02+
mv02+ ![]() 2mu2=
2mu2= ![]() mv12+
mv12+ ![]() 2mv22
2mv22
��ã� ![]() ��
�� ![]()
�𣺻���C���ص�A�ĵ�ʱAB����Ϊ ![]() ��C���ٶ�Ϊ
��C���ٶ�Ϊ ![]() ��
��
��3���⣺����C��A�ĵ�ʱ���A�����˶����Ե��ٶ����ң��������A�������ٶ�Ϊ��
Vx=v1��v2
��Բ���˶����ɣ�F��mg= ![]()
��ã�F=4mg
�𣺻���C���ص�A�ĵ�ʱC��A��ѹ��Ϊ4mg��
����������1��AB��ɵ�ϵͳˮƽ�������������㶯���غ㣬����û���B��A��ײ����ٶ�ʱ�ٶȣ�����ABCΪϵͳˮƽ�������غ㣬���C����A����ߵ�ʱABC���ٶȣ��ٸ��������غ����B��Cһ�������˶����ٶȣ���2�����ݶ����غ㶨�����е���غ㼴���������C���ص�A�ĵ�ʱAB�����C���ٶ�Ϊ���٣�3��C��AB����Ҫ�˶�����C�����A�����˶������������ٶȣ�Ȼ����ţ�ٵڶ����ɼ��������
�����㾫�����������⣬������Ҫ�˽�������(����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ��������)����Ҫ���չ��ܹ�ϵ(��ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1)�����֪ʶ���Ǵ���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�