题目内容
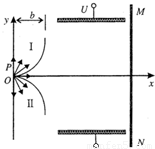
如图所示,位于坐标原点O处的一粒子源P,在xoy平面内以同一速率v同时向y轴右侧(含y轴)各个方向发射相同的正粒子,粒子质量为m、电荷量为q.在由y轴和上、下两个与x轴相切于原点O、半径为b的 圆弧所围成的区域(含边界)中,分别存在垂直于xoy平面的匀强磁场Ⅰ、Ⅱ.经过磁场区域后,粒子均沿x轴正方向运动,然后全部射人正对放置的金属平板之间,两平板垂直于y方向且关于x轴对称,板间距离为d,在金属板右侧放置垂直于x轴且足够大的接收屏MN.若两板间加上大小为U的恒定电压,只在板间形成沿y轴负方向的匀强电场,不计粒子重力及粒子间的相互作用.那么
圆弧所围成的区域(含边界)中,分别存在垂直于xoy平面的匀强磁场Ⅰ、Ⅱ.经过磁场区域后,粒子均沿x轴正方向运动,然后全部射人正对放置的金属平板之间,两平板垂直于y方向且关于x轴对称,板间距离为d,在金属板右侧放置垂直于x轴且足够大的接收屏MN.若两板间加上大小为U的恒定电压,只在板间形成沿y轴负方向的匀强电场,不计粒子重力及粒子间的相互作用.那么(1)磁场Ⅰ、Ⅱ的磁感应强度大小是多少?方向如何?
(2)若全部粒子均能打在接收屏上,金属板的最大长度是多少?此时粒子在接收屏上的分布范围是多大?
(3)对由粒子源同一时刻发出的粒子而言,若沿x轴运动的粒子恰能从板间出射,且在其出射瞬间撤去电场,那么,打在接收屏上的粒子在进出金属板间的过程中,y方向动量变化的最小值是多少?
(2)、首先根据运动学公式,在竖直方向上可求出带电粒子的运动时间,在水平方向上,粒子一直做匀速直线运动,便可求出粒子在该时间内的水平位移,即为金属板的最大长度.
(3)、由运动学公式表示出沿x轴入射的粒子从板间射出的时间t2与竖直方向的位移的关系,再分析所有粒子到达金属边间的最大时间差△t,便可得到动量变化△p的表达式,根据t2-△t取值,可分析粒子沿y方向动量变化的最小值.
解答:解:
(1)、磁场Ⅰ的磁感应强度为B1,方向垂直纸面向外,由题意可知,粒子在磁场中做圆周运动的半径是b,则有:

得:

磁场Ⅱ的磁感应强度为B2,方向垂直纸面向内,由题意可知有:

(2)、由y=-b处入射的粒子恰能从金属板间射出,所用的时间为t1,由牛顿第二定律可得粒子在y轴方向的加速度为:

由运动学公式有:

金属板的最大长度为:
Lmax=vt1
由以上各式可得:
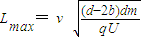
所有粒子经电场都沿y的负方向偏移同样大小的量值,所以粒子在MN屏上的y方向分布范围为:
△yMN=2b
(3)、沿x轴入射的粒子恰能从板间射出,所用的时间为t2,则由运动学公式有:

由y=b处入射的粒子与y=0处入射的粒子刚到达金属板间的时间差最大,为:

y=b处入射的粒子在y方向的动量变化最小,其值为△p,由动量定理得:

当t2-△t>0时

当t2-△t≤0时,粒子不经电场加速
△p=0
答:(1)磁场Ⅰ、Ⅱ的磁感应强度大小都为
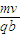 .方向分别为垂直纸面向外和向里.
.方向分别为垂直纸面向外和向里.(2)若全部粒子均能打在接收屏上,金属板的最大长度是
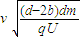 ,此时粒子在接收屏上的分布范围是2d.
,此时粒子在接收屏上的分布范围是2d.(3)y方向动量变化的最小值是0.
点评:此题考察到了两方面的问题,一是在磁场中的偏转,一是在电场中的偏转.
对于带点粒子在磁场中的偏转,往往联系临界和多解问题,当粒子速度大小不变,速度方向变化;此时由于速度大小不变,则所有粒子运动的轨道半径相同,但不同粒子的圆心位置不同,其共同规律是:所有粒子的圆心都在以入射点为圆心,以轨道半径为半径的圆上,从而找出动圆的圆心轨迹,再确定运动轨迹的临界点.
粒子在电场中的偏转,把运动沿电场的方向和垂直于电场的方向进行分解,一是做初速度为零的匀加速直线运动,一是做匀速直线运动,分别运用运动学公式进行列式求解即可.

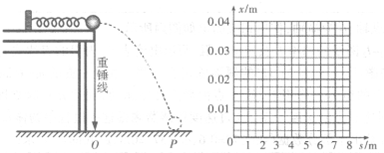
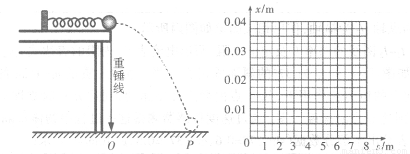
为了研究轻质弹簧的弹性势能与弹簧压缩量的关系,某实验小组的实验装置如图所示,光滑水平桌面距地面高为h,一轻质弹簧左端固定,右端与质量为m的小钢球接触,弹簧处于原长。将小球向左推,压缩弹簧一段距离后由静止释放,弹簧将小球沿水平方向推出,小球落到位于水平地面的记录纸上,留下痕迹,已知重力加速度为g
(1) 某次实验测得小球的落点P到O点的距离为S,那么由理论分析得到小球释放前压缩弹簧的弹性势能Ep与h、s、mg之间的关系式为____________________;
(2) 改变弹簧压缩量进行多次实验,测量数据如下表所示,请在坐标纸上做出x-s图象。
| 弹簧压缩量x/m | 0.010 | 0.015 | 0.020 | 0.025 | 0.030 | 0.035 |
| 小球飞行水平距离s/m | 2.0 | 3.0 | 4.1 | 5.9 | 6.0 | 7.0 |
(3) 由图象得出x与s的关系式为_______________;由实验得到弹簧弹性势能Ep与弹簧压缩量x之间的关系式为______________。
为了研究轻质弹簧的弹性势能与弹簧压缩量的关系,某实验小组的实验装置如图所示,光滑水平桌面距地面高为h,一轻质弹簧左端固定,右端与质量为m的小钢球接触,弹簧处于原长。将小球向左推,压缩弹簧一段距离后由静止释放,弹簧将小球沿水平方向推出,小球落到位于水平地面的记录纸上,留下痕迹,已知重力加速度为g
(1) 某次实验测得小球的落点P到O点的距离为S,那么由理论分析得到小球释放前压缩弹簧的弹性势能Ep与h、s、mg之间的关系式为____________________;
(2) 改变弹簧压缩量进行多次实验,测量数据如下表所示,请在坐标纸上做出x-s图象。
|
弹簧压缩量x/m |
0.010 |
0.015 |
0.020 |
0.025 |
0.030 |
0.035 |
|
小球飞行水平距离s/m |
2.0 |
3.0 |
4.1 |
5.9 |
6.0 |
7.0 |
(3) 由图象得出x与s的关系式为_______________;由实验得到弹簧弹性势能Ep与弹簧压缩量x之间的关系式为______________。

(1)某次实验测得小球的落点P到O点的距离为s,那么由理论分析得到小球释放前压缩弹簧的弹性势能Ep与h、s、mg之间的关系式为______;
(2)改变弹簧压缩量进行多次实验,测量数据如下表所示,请在坐标纸上做出x-s图象.
| 弹簧压缩量x/m | 0.010 | 0.015 | 0.020 | 0.025 | 0.030 | 0.035 |
| 小球飞行水平距离s/m | 2.0 | 3.0 | 4.1 | 5.9 | 6.0 | 7.0 |