题目内容
【题目】如图所示,在一匀强磁场中有三个带电粒子,其中1和2为质子,3为α粒子(![]() He)的径迹。它们在同一平面内沿逆时针方向做匀速圆周运动,三者轨道半径r1>r2>r3并相切于P点,设T、v、a、t分别表示它们做圆周运动的周期、线速度、向心加速度以及各自从经过P点算起到第一次通过图中虚线MN所经历的时间,则( )
He)的径迹。它们在同一平面内沿逆时针方向做匀速圆周运动,三者轨道半径r1>r2>r3并相切于P点,设T、v、a、t分别表示它们做圆周运动的周期、线速度、向心加速度以及各自从经过P点算起到第一次通过图中虚线MN所经历的时间,则( )
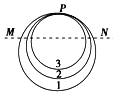
A. T1=T2<T3 B. v1>v2>v3 C. a1>a2>a3 D. t1>t2>t3
【答案】ABC
【解析】
根据带电粒子在匀强磁场中做匀速圆周运动,由洛伦兹力提供向心力可得半径公式,同时推出周期公式和时间公式,根据牛顿第二定律得到加速度的公式,再进行分析。
设带电粒子的质量和电量分别为m、q,则带电粒子在匀强磁场中做匀速圆周运动时周期为![]() ,T与比荷成反比,质子与α粒子的比荷之比为2:1,则有
,T与比荷成反比,质子与α粒子的比荷之比为2:1,则有![]() ,故A正确。带电粒子在匀强磁场中做匀速圆周运动时半径为
,故A正确。带电粒子在匀强磁场中做匀速圆周运动时半径为![]() ,则
,则![]() ,对粒子1和2 ,其比荷相等,则半径越大速度越大,故
,对粒子1和2 ,其比荷相等,则半径越大速度越大,故![]() ;对粒子2和3,粒子2的比荷和半径均比粒子3大,故
;对粒子2和3,粒子2的比荷和半径均比粒子3大,故![]() 故B正确。粒子的加速度为
故B正确。粒子的加速度为![]() ,同理
,同理![]() ,故C正确。由图看出粒子2的速度偏向角大于粒子1的速度偏向角,根据轨迹所对的圆心角等于速度偏向角,可知粒子2轨迹的圆心角大于粒子1轨迹的圆心角,所以粒子2的运动时间大于粒子1的运动时间,即
,故C正确。由图看出粒子2的速度偏向角大于粒子1的速度偏向角,根据轨迹所对的圆心角等于速度偏向角,可知粒子2轨迹的圆心角大于粒子1轨迹的圆心角,所以粒子2的运动时间大于粒子1的运动时间,即![]() ;同理可得,粒子3轨迹的圆心角大于粒子2轨迹的圆心角,同时由于
;同理可得,粒子3轨迹的圆心角大于粒子2轨迹的圆心角,同时由于![]() 可知
可知![]() ,故有
,故有![]() ,则
,则![]() ,故D错误。
,故D错误。

练习册系列答案
相关题目