题目内容
20．
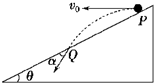如图所示，从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球，落在斜面上某处Q点，小球落在斜面上的速度与斜面的夹角α，若把初速度变为2v0，小球仍落在斜面上，则（ ）| A． | 空中的运动时间变为原来的2倍 | B． | 夹角α不变 | ||
| C． | 夹角α将变大 | D． | PQ间距一定是原来间距的2倍 |
分析 小球落在斜面上，根据竖直位移与水平位移的关系求出小球在空中的运动时间，从而得出PQ间的变化．结合速度方向与水平方向夹角正切值和位移与水平方向夹角正切值的关系，判断夹角与初速度的关系．
解答 解：A、根据tanθ=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{{2v}_{0}}$，得t=$\frac{2{v}_{0}tanθ}{g}$，则初速度变为原来的2倍，则小球在空中的运动时间变为原来的2倍．故A正确；
BC、小球落到斜面上时速度与水平方向夹角的正切值 tanβ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{gt}{{v}_{0}}$=2tanθ，θ一定，则β一定，即小球落到斜面上时速度与水平方向夹角不变，所以两个角度之差，即α不变，与初速度无关．故B正确，C错误；
D、根据x=v0t=$\frac{2{v}_{0}^{2}tanθ}{g}$知，初速度变为原来的2倍，则水平位移变为原来的4倍，则PQ间距变为原来的4倍．故D错误．
故选：AB．
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，知道某时刻速度方向与水平方向夹角正切值是位移与水平方向夹角正切值的2倍这一结论．
练习册系列答案
相关题目
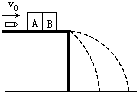如图所示，两个质量都是M=0.4kg的砂箱A、B，并排放在光滑的水平桌面上，一颗质量为m=0.1kg的子弹以v0=140m/s的水平速度射向A，射穿A后，进入B并同B一起运动，测得A、B落地点到桌边缘的水平距离之比为1：2，求子弹刚穿出砂箱A时的速度v1及砂箱A、B离开桌面时的速度是多大？
15．某船在静水中的划行速度v1=5m/s，要渡过d=30m宽的河，河水的流速v2=4m/s，下列说法正确的是（ ）
| A． | 该船渡河所用时间至少是7.5s | |
| B． | 该船的航程至少是30m | |
| C． | 河水流速越大，渡河的时间越长 | |
| D． | 该船以最短时间渡河时的位移大小为50m |
如图，一架在H=2000m的高空以v0=100m/s速度直线飞行的老式轰炸机投放两枚炸弹分别轰炸山脚和山顶的目标A和B，已知山顶高h=1280m，山脚和山顶的目标A和B的水平距离L=800m，不计炸弹受到的空气阻力，g=10m/s2，求：
（1）图示为研究平抛运动的演示实时，用小锤去打击弹性金属片，A球水平飞出，同时B球被松开做自由落体运动，两球同时落到地面．这个实验B