题目内容
【题目】有一个摆长为L的单摆（摆球可视为质点，摆线的质量不计），在过悬挂点的竖直线上距悬挂点O的距离为x处（
）的C点有一个固定的钉子，如图所示，当摆摆时，摆线会受到钉子的阻挡，当L一定而x取不同值时，阻挡后摆球的运动情况将不同，现将摆拉到位于竖直线的左方（摆球的高度不超过O点）然后放手，令其自由摆动，如果摆线被钉子阻挡后，摆球恰能够击中钉子，试求x的最小值。
【答案】
【解析】摆线受阻后在一段时间内摆球作圆周运动，若摆球的质量为m，
则摆球受重力mg和摆线拉力T的作用，设在这段时间内任一时刻的速度为v，如图所示：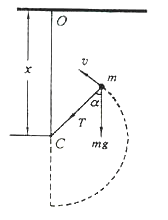
用
表示此时摆线与重力方向之间的夹角，
由牛顿第二定律得：
，
运动过程中机械能守恒，令
表示摆线在起始位置时与竖直方向的夹角，取O点为势能零点，由机械能守恒定律得：
，
摆受阻后，如果后来摆球能击中钉子，则必定在某位置时摆线开始松弛，
此时
，此后摆球仅在重力作用下作斜抛运动，设在该位置时摆球速度
，摆线与竖直线的夹角
，
解得：
，
，
要求作斜抛运动的摆球击中C点，
则应满足下列关系式：
，
，
解得：
，
，
，越大，
越小，
越小，最大值为
，由此可求得x的最小值：
，
则：
。
练习册系列答案
相关题目
