题目内容
12.用单摆测重力加速度,直接测量的物理量是摆长,用直接测量量表达重力加速度,其关系式是g=$\frac{4{π}^{2}(L+\frac{d}{2})}{{T}^{2}}$.分析 单摆的摆长等于摆线的长度与摆球半径之和,求得摆长,由单摆周期公式求解g的表达式.
解答 解:据单摆的振动周期T=2π$\sqrt{\frac{L}{g}}$ 和摆长为:L+$\frac{d}{2}$ 得到:g=$\frac{4{π}^{2}(L+\frac{d}{2})}{{T}^{2}}$;
故答案为:摆长,g=$\frac{4{π}^{2}(L+\frac{d}{2})}{{T}^{2}}$.
点评 解决本题的关键掌握测量重力加速度的原理:单摆的周期公式,明确操作的注意事项,比如:计时起点是平衡位置和重力加速度的表达式.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
5.在研究下列哪些运动时,被指定的物体可以视为质点( )
| A. | 研究地球自转时的地球 | B. | 研究地球绕太阳的公转时的地球 | ||
| C. | 研究车轮自转情况时的车轮 | D. | 研究运动员的跑步动作时的运动员 |
3.在“练习使用打点计时器”的实验中,下列说法正确的是( )
| A. | 打点前,小车应停在靠近打点计时器的位置 | |
| B. | 实验时,要先接通电源,待计时器开始打点再释放小车 | |
| C. | 实验中应使小车速度尽量小些 | |
| D. | 点迹记录了物体在不同时刻的位置和某段时间内的位移,反映了物体的运动情况 |
7.平行金属板水平放置,板间距为0.6cm,两板接上6×103V电压,板间有一个带电液滴质量为4.8×10-10g,处于静止状态,场强的大小是( )
| A. | 1×106 N/C | B. | 1×104 N/C | C. | 3×106 N/C | D. | 3×104 N/C |
4.如图所示,小球处于静止状态,下列选项中正确的是( )
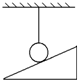

| A. | 只受重力 | B. | 受拉力、重力、支持力 | ||
| C. | 受拉力和重力 | D. | 受拉力、重力、摩擦力 |
1. 如图所示,电流表、电压表均为理想电表,L为小电珠.R为滑动变阻器,电源电动势为E,内阻为r.现将开关S闭合,当滑动变阻器滑片P向左移动时,下列结论正确的是( )
如图所示,电流表、电压表均为理想电表,L为小电珠.R为滑动变阻器,电源电动势为E,内阻为r.现将开关S闭合,当滑动变阻器滑片P向左移动时,下列结论正确的是( )
 如图所示,电流表、电压表均为理想电表,L为小电珠.R为滑动变阻器,电源电动势为E,内阻为r.现将开关S闭合,当滑动变阻器滑片P向左移动时,下列结论正确的是( )
如图所示,电流表、电压表均为理想电表,L为小电珠.R为滑动变阻器,电源电动势为E,内阻为r.现将开关S闭合,当滑动变阻器滑片P向左移动时,下列结论正确的是( )| A. | 电流表示数变小,电压表示数变大 | B. | 小电珠L变暗 | ||
| C. | 电容器C上电荷量减小 | D. | 电源的总功率变小 |
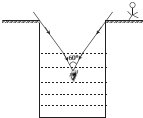 如图所示,某潜水员在检查装有透明液体的圆柱体容器,当潜水员的眼睛在容器中心轴位置且在液面下h2=1m处时,他看到容器口处所有景物都出现在一个顶角为60°的倒立圆锥里,已知容器口距离容器液面的距离h1=1m,圆柱体的横切面半径r=$\frac{4}{3}$$\sqrt{3}$m.
如图所示,某潜水员在检查装有透明液体的圆柱体容器,当潜水员的眼睛在容器中心轴位置且在液面下h2=1m处时,他看到容器口处所有景物都出现在一个顶角为60°的倒立圆锥里,已知容器口距离容器液面的距离h1=1m,圆柱体的横切面半径r=$\frac{4}{3}$$\sqrt{3}$m. 如图所示,在光滑水平面上,物体受两个相互垂直的大小分别为F1=3N和F2=4N的恒力,其合力在水平方向上,从静止开始运动10m,在这一过程中力F1做的功为18J;力F2做的功为32J;合力F做的功为50J.
如图所示,在光滑水平面上,物体受两个相互垂直的大小分别为F1=3N和F2=4N的恒力,其合力在水平方向上,从静止开始运动10m,在这一过程中力F1做的功为18J;力F2做的功为32J;合力F做的功为50J.