题目内容
2011年7月23日20时34分在温州方向双屿路段下岙路,发生了严重的动车追尾事故,此次事故造成六节车厢脱轨。现假设有一列快车正以60m/s的速度在平直的铁轨上行驶时,发现前面1000m处有一货车正以18m/s的速度匀速同向行驶,快车立即合上制动器,以2 m/s2的加速度做匀减速直线运动,试判断两车是否发生撞车事故.
不会发生撞车事故
分析:在速度相等前,快车的速度大于货车的速度,两车的距离越来越小,若不相撞,速度相等后,快车的速度小于货车的速度,两车的距离越来越小,知两车若相撞,只能在速度相等前或相等时相撞.求出速度相等时,两车的位移,根据位移关系,判断两车是否相撞.
解答:解:设在快车制动ts后两车达到共同速度
由V快=V货 有:υ0-at=υ货t=21s
在此过程中:S快=υ0t-at2/2=819m
S贷=υt=378m
由于 S快<S货+S0
所以两车不会发生撞车事故.
点评:解决本题的关键知道速度大者减速追速度小者,若相撞,只能在速度相等之时或速度相等前相撞,若不相撞,速度相等时有最小距离.
解答:解:设在快车制动ts后两车达到共同速度
由V快=V货 有:υ0-at=υ货t=21s
在此过程中:S快=υ0t-at2/2=819m
S贷=υt=378m
由于 S快<S货+S0
所以两车不会发生撞车事故.
点评:解决本题的关键知道速度大者减速追速度小者,若相撞,只能在速度相等之时或速度相等前相撞,若不相撞,速度相等时有最小距离.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
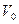 匀速行驶。
匀速行驶。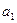 =-5m/s2,汽车刚好在路障前面停下,求汽车原来的速度
=-5m/s2,汽车刚好在路障前面停下,求汽车原来的速度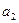 =-3m/s2,初速度不变,为使汽车不撞上路障,司机必须比加速度是
=-3m/s2,初速度不变,为使汽车不撞上路障,司机必须比加速度是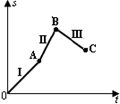
 车在此行驶速度的情况下刹车需要经过1815m才能够停止,试求:
车在此行驶速度的情况下刹车需要经过1815m才能够停止,试求: