Question

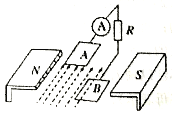
【题目】一能屏蔽高能粒子辐射的长方体铅盒，如图甲所示，铅盒左侧面正中心O处有一放射源，它可向外辐射速率均为v=1×107m/s的正粒子，粒子通过铅盒右侧面狭缝MQ射入一平行边界的匀强磁场中，粒子均不能从磁场的右边界射出。图乙为该装置的截面简化图，截面MNPQ位于垂直磁场的平面内。已知PQ=0.3m，NP=0.6m，该粒子质量m=4×10-27kg，电量q=8×10-19C，磁场的磁感应强度B=0.5 T，方向垂直于纸面向里。求

(1)粒子在磁场中运动的半径R；

(2)粒子从O点射出到离开磁场左边界的最长时间t；

(3)若粒子放射源可以处在NP的任意位置，为了使粒子均不能从磁场的右边界射出，磁场区域的宽度d至少多大？()

Answer 1

【答案】(1) 0.1 m (2) (3) 0.188m

【解析】（1）由R＝，代入数据解得：

（2）经判断从Q点射入磁场的粒子在铅盒及磁场中的时间都最长，分别设为t1和t2，总时间也最长．
OQ=0.3m

在磁场中逆时针旋转3T/4离开磁场左边界

总时间
（3）经判断，当放射源处于N点时，磁场区域的宽度d最大．
由几何关系d=R（1+cosθ）
cosθ＝
解得d=0.188m