��Ŀ����
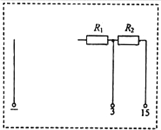
����Ŀ��ijͬѧΪ�˲ⶨľ����б���Ķ�Ħ�����������ò������о�ľ����б���ϵ��˶������װ����ͼ����ʾ����ʹľ���Գ��ٶ�v0=4m/s���ٶ��������=30����б���ϻ��������»��������㣬��ͬʱ��ʼ��¼���ݣ��������ֻ�����ľ��ӿ�ʼ�ϻ�����ߵ��v��tͼ����ͼ����ʾ��gȡ10m/s2����
��1���ϻ������еļ��ٶȵĴ�Сa1��
��2��ľ����б���Ķ�Ħ����������
��3��ľ��ص�������ʱ���ٶȴ�Сv��
���𰸡���1���ϻ������еļ��ٶȵĴ�С![]() ��
��
��2��ľ����б���Ķ�Ħ��������=0.35��
��3��ľ��ص�������ʱ���ٶȴ�Сv=2m/s��
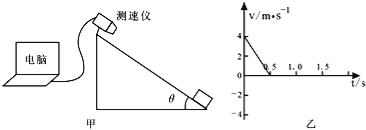
�������������������1����v��tͼ���������ϻ����̵ļ��ٶȣ�
��2����ţ�ٵڶ����ɿ��Եõ�Ħ��������
��3�����˶�ѧ�ɵ��ϻ����룬���¾�����ȣ���ţ�ٵڶ����ɿɵ��»��ļ��ٶȣ������˶�ѧ�ɵ��»�����������ٶȣ�
�⣺��1������ͼ�ҿ�֪��ľ�龭0.5s������ߵ㣬�ɼ��ٶȶ���ʽ![]() �У�
�У�
�ϻ������м��ٶȵĴ�С��
![]()
��2���ϻ���������б�������������ķ�����Ħ��������ţ�ٵڶ�����F=ma���ϻ��������У�
mgsin��+��mgcos��=ma1
�������ݵã���=0.35��
��3���»��ľ�������ϻ��ľ��룺
x=![]() =
=![]() m=1m
m=1m
�»�Ħ���������Ϊ���ϣ���ţ�ٵڶ�����F=ma�ã�
�»������У�mgsin�ȩ���mgcos��=ma2
��ã�![]() =2m/s2
=2m/s2
�»�����������ٶȴ�СΪ��v=![]()
������ã�v=2m/s
�𣺣�1���ϻ������еļ��ٶȵĴ�С![]() ��
��
��2��ľ����б���Ķ�Ħ��������=0.35��
��3��ľ��ص�������ʱ���ٶȴ�Сv=2m/s��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�