题目内容
4.空间中有相距1m的两质点a、b,当a处于波峰时,b质点恰好处于平衡位置且向上振动,已知质点a振动周期为2s,则该波的波速为$\frac{2}{4n+1}$m/s,(n=0,1,2,3…);或$\frac{2}{4n+3}$m/s,(n=0,1,2,3…)..分析 根据a、b两点的状态关系,确定出波长与ab间的距离关系,求出波长的通项,再求出波速.分波向左和向右传播两种情况.
解答  解:当波向右传播时,由波的传播方向和质点的振动方向可知,a、b之间平衡位置的距离最少相差$\frac{1}{4}$λ,如图①所示,则有:
解:当波向右传播时,由波的传播方向和质点的振动方向可知,a、b之间平衡位置的距离最少相差$\frac{1}{4}$λ,如图①所示,则有:
△x=(n+$\frac{1}{4}$)λ=1m
得:λ=$\frac{4}{4n+1}$m,(n=0,1,2,3…)
波速v=$\frac{λ}{T}$=$\frac{2}{4n+1}$m/s,(n=0,1,2,3…);
同理当波向左传播时,如图②所示,则△x=(n+$\frac{3}{4}$)=1m
可得 λ=$\frac{4}{4n+3}$m,v=$\frac{2}{4n+3}$m/s,(n=0,1,2,3…)
故答案为:$\frac{2}{4n+1}$m/s,(n=0,1,2,3…);或$\frac{2}{4n+3}$m/s,(n=0,1,2,3…).
点评 解决本题的关键画出波形,确定ab间的距离与波长的关系,要注意波的双向性,不能漏解.

练习册系列答案
相关题目
12.如图所示为同一实验中甲、乙两个单摆的振动图象,由图象可知( )
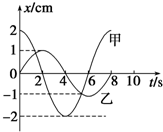

| A. | 两摆球质量相等 | |
| B. | 两单摆的摆长相等 | |
| C. | 两单摆相位相差为$\frac{π}{2}$ | |
| D. | 在相同的时间内,两摆球通过的路程总有s甲=2s乙 |
19.当人听到声音频率越来越低时,不可能是因为( )
| A. | 声源和人都是静止的,但是声源振动频率越来越低 | |
| B. | 人静止,声源远离人做匀速直线运动,且声源的频率不变 | |
| C. | 人静止,声源远离人做匀加速直线运动,且声源的频率不变 | |
| D. | 声源静止,人远离声源做匀加速直线运动,且声源的频率不变 |
9.目前雷达发射的电磁波频率多在200MHz至1 000MHz的范围内,下列关于雷达和电磁波说法错误的是( )
| A. | 真空中上述雷达发射的电磁波的波长范围在0.3m至1.5m之间 | |
| B. | 电磁波是由恒定不变的电场或磁场产生的 | |
| C. | 测出从发射电磁波到接收反射波的时间间隔可以确定雷达和目标的距离 | |
| D. | 波长越短的电磁波,反射性能越强 |
16.下列说法正确的是( )
| A. | 物体所受到的合外力越大,其速度改变量也越大 | |
| B. | 物体所受到的合外力变化,其速度的变化率一定变化 | |
| C. | 物体所受到的合外力不变(F合≠0),其运动状态就不改变 | |
| D. | 物体所受到的合外力减小时,物体的速度可能正在增大 |
 如图所示,半径为R的光滑半圆环AB竖直固定在光滑水平地面上,质量为m的小球以某一速度υ0从A点进入半圆环,经最高点B水平向左飞出(不计空气阻力)求:
如图所示,半径为R的光滑半圆环AB竖直固定在光滑水平地面上,质量为m的小球以某一速度υ0从A点进入半圆环,经最高点B水平向左飞出(不计空气阻力)求:
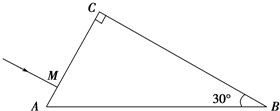 如图所示,截面为直角三角形ABC,∠B=30°,斜边AB=a.棱镜材料的折射率为,n=$\sqrt{2}$.在此截面所在的平面内,一条光线在距A点为$\frac{a}{8}$处的M点垂直AC射入棱镜,不考虑光线沿原路返回的情况,光线从玻璃砖的BC边射出.求:
如图所示,截面为直角三角形ABC,∠B=30°,斜边AB=a.棱镜材料的折射率为,n=$\sqrt{2}$.在此截面所在的平面内,一条光线在距A点为$\frac{a}{8}$处的M点垂直AC射入棱镜,不考虑光线沿原路返回的情况,光线从玻璃砖的BC边射出.求: