题目内容
14.宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其他星体对它们的引力作用.已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个顶点上,并沿外接于等边三角形的圆轨道运行.设每个星体的质量均为m.(1)试求第一种形式下,星体运动的线速度v和周期T.
(2)假设两种形式下星体的运动周期相同,试求第二种形式下星体间的距离r应为多少?[设三个星体做圆周运动的半径为R′(未知)].
分析 明确研究对象,对研究对象受力分析,找到做圆周运动所需向心力的来源.
(1)运行的任一卫星受到中心星体和另一个转动的星体的万有引力作用,合力充当向心力,列式求解即可;
(2)对其中一个星体受力分析,根据平行四边形定则求出合力,有合力充当向心力列式即可.
解答 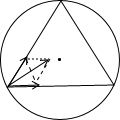 解:(1)在第一种形式下,以某个运动星体为研究对象,根据牛顿第二定律和万有引力定律有:
解:(1)在第一种形式下,以某个运动星体为研究对象,根据牛顿第二定律和万有引力定律有:
${F_1}=G\frac{m^2}{R^2}$,${F_2}=G\frac{m^2}{{{{(2R)}^2}}}$${F_1}+{F_2}=m\frac{v^2}{R}$,
解得:v=$\sqrt{\frac{5Gm}{4R}}$,
周期:$T=\frac{2πR}{v}$,解得:T=4π$\sqrt{\frac{{R}^{3}}{5Gm}}$;
(2)设第二种形式下,三个星体做圆周运动的半径为:$R'=\frac{{\frac{r}{2}}}{cos30°}$,
由于星体做圆周运动所需的向心力靠其他两个星体的万有引力的合力提供,由力的合成和牛顿运动定律有:
${F_合}=2G\frac{m^2}{r^2}cos30°=m\frac{{4{π^2}}}{T^2}R'$,
解得:r=$\root{3}{2.4}$R;
答:(1)第一种形式下,星体运动的线速度v为:$\sqrt{\frac{5Gm}{4R}}$,周期T为:4π$\sqrt{\frac{{R}^{3}}{5Gm}}$.
(2)假设两种形式下星体的运动周期相同,第二种形式下星体间的距离r应为:$\root{3}{2.4}$R.
点评 本题考查了万有引力定律的应用,万有引力定律和牛顿第二定律是力学的重点,在本题中有些同学找不出什么力提供向心力,关键在于进行正确受力分析.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
4.在光滑的水平面上,并排放着质量相等的物体A和B,并静止于水平面上,现用水平恒力F推A,此时沿F方向给B一个瞬时冲量I,当A追上B时,它们运动的时间是( )
| A. | $\frac{F}{2I}$ | B. | $\frac{I}{F}$ | C. | $\frac{2I}{F}$ | D. | $\frac{I}{2F}$ |
5.如图是一汽车在平直路面上启动的速度-时间图象,t1时刻起汽车的功率保持不变.由图象可知( )


| A. | 0~t1时间内,汽车的牵引力增大,加速度增大,功率增大 | |
| B. | 0~t1时间内,汽车的牵引力不变,加速度不变,功率减小 | |
| C. | t1~t2时间内,汽车的牵引力减小,加速度减小 | |
| D. | t1~t2时间内,汽车的牵引力不变,加速度减小 |
9.矩形线圈在匀强磁场中匀速转动,从中性面开始转动180°角的过程中,平均感应电动势和最大感应电动势之比为( )
| A. | 2:π | B. | 1:2 | C. | 2π:1 | D. | 2:1 |
19. 如图所示,理想变压器原、副线圈的匝数比为20:1,b接原线圈的中心抽头,电压表和电流表均为理想电表.从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u=220$\sqrt{2}$sin100πt(V),则( )
如图所示,理想变压器原、副线圈的匝数比为20:1,b接原线圈的中心抽头,电压表和电流表均为理想电表.从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u=220$\sqrt{2}$sin100πt(V),则( )
 如图所示,理想变压器原、副线圈的匝数比为20:1,b接原线圈的中心抽头,电压表和电流表均为理想电表.从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u=220$\sqrt{2}$sin100πt(V),则( )
如图所示,理想变压器原、副线圈的匝数比为20:1,b接原线圈的中心抽头,电压表和电流表均为理想电表.从某时刻开始在原线圈c、d两端加上交变电压,其瞬时值表达式为u=220$\sqrt{2}$sin100πt(V),则( )| A. | 当单刀双掷开关与b连接时,电压表的示数为22V | |
| B. | 原线圈和副线圈中交变电流的频率之比为20:l | |
| C. | 当单刀双掷开关由a扳向b后,电压表和电流表的示数均变大 | |
| D. | 单刀双掷开关与a连接,在滑动变阻器触头P向上移动的过程中,电压表和电流表的示数均变小 |
6.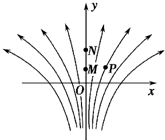 如图所示.一电场的电场线分布关于y轴(沿竖直方向)对称,OMN是y轴上的三个点,且OM=MN,P点在y轴的右侧,MP⊥ON,则( )
如图所示.一电场的电场线分布关于y轴(沿竖直方向)对称,OMN是y轴上的三个点,且OM=MN,P点在y轴的右侧,MP⊥ON,则( )
 如图所示.一电场的电场线分布关于y轴(沿竖直方向)对称,OMN是y轴上的三个点,且OM=MN,P点在y轴的右侧,MP⊥ON,则( )
如图所示.一电场的电场线分布关于y轴(沿竖直方向)对称,OMN是y轴上的三个点,且OM=MN,P点在y轴的右侧,MP⊥ON,则( )| A. | M点的电势比P点的电势高 | |
| B. | 将负电荷由O点移动到P点,电场力做正功 | |
| C. | MN 两点间的电势差大于O、M两点间的电势差 | |
| D. | 在O点静止释放一带正电粒子,该粒子将沿y轴做加速直线运动 |
3.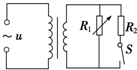 如图所示为一理想变压器,在原线圈输入电压不变的条件下,要提高变压器的输入功率,可采用的方法是( )
如图所示为一理想变压器,在原线圈输入电压不变的条件下,要提高变压器的输入功率,可采用的方法是( )
 如图所示为一理想变压器,在原线圈输入电压不变的条件下,要提高变压器的输入功率,可采用的方法是( )
如图所示为一理想变压器,在原线圈输入电压不变的条件下,要提高变压器的输入功率,可采用的方法是( )| A. | 只增加原线圈的匝数 | B. | 只增加副线圈的匝数 | ||
| C. | 只增大R1的电阻值 | D. | 断开开关S |
