题目内容
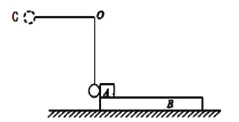
【题目】如图所示,平行粗糙导轨固定在绝缘水平桌面上,间距L=0.2 m,导轨左端接有R=1 Ω的电阻,质量为m=0.1 kg的粗糙导棒ab静置于导轨上,导棒及导轨的电阻忽略不计。整个装置处于磁感应强度B=0.5 T的匀强磁场中,磁场方向垂直导轨向下。现外力F作用在导棒ab上使之一开始做匀加速运动,且外力F随时间变化关系如图乙所示,重力加速度g=10 m/s2,试求解以下问题:
(1)比较导棒a、b两点电势的高低;
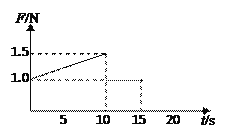
(2)前10 s导棒ab的加速度;
(3)若整个过程中通过R的电荷量为65 C,则导体棒ab运动的总时间是多少?

【答案】(1)a点电势较高(2)5m/s2(3)22s
【解析】(1)据右手定则知,a点电势较高
(2)由于导棒一开始匀加速,对ab用牛顿第二定律:
![]()
![]()
![]()
综上得, ![]()
据图像可知前10s,F-t图线斜率为0.05,即 ![]()
代入数据解得:a=5m/s2
(3)当t=0时,f+ma=1N,则f=0.5N
10s时导棒的速度v1=at1=50m/s
此时安培力 ![]()
由于F=1N,且此时![]() ,故10s-15s内导棒做匀速直线运动
,故10s-15s内导棒做匀速直线运动
0-15s内导棒ab的位移![]()
通过R的电荷量![]()
F为0后,导棒做减速运动直到停止过程中通过R的电量:
![]()
对导棒ab应用动量定理:- ![]()
解得t3=7s
则总运动时间:t=t1+t2+t3=22s

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目