题目内容
7.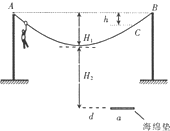 在“极限”运动会中,有一个在钢索桥上的比赛项目.如图所示,总长为L=10m的均匀粗钢丝绳固定在等高的A、B处,钢丝绳最低点与固定点A、B的高度差为H1=0.3m,动滑轮起点在A处,并可沿钢丝绳滑动,钢丝绳最低点距离水面也为H2=3.2m.若质量为m的人抓住滑轮下方的挂钩由A点静止滑下,最远能到达右侧C点,C、B间钢丝绳相距为L′=2m,高度差为h=0.1m.若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为h,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变.g取10m/s2.求:
在“极限”运动会中,有一个在钢索桥上的比赛项目.如图所示,总长为L=10m的均匀粗钢丝绳固定在等高的A、B处,钢丝绳最低点与固定点A、B的高度差为H1=0.3m,动滑轮起点在A处,并可沿钢丝绳滑动,钢丝绳最低点距离水面也为H2=3.2m.若质量为m的人抓住滑轮下方的挂钩由A点静止滑下,最远能到达右侧C点,C、B间钢丝绳相距为L′=2m,高度差为h=0.1m.若参赛者在运动过程中始终处于竖直状态,抓住滑轮的手与脚底之间的距离也为h,滑轮与钢丝绳间的摩擦力大小视为不变,且摩擦力所做功与滑过的路程成正比,不计参赛者在运动中受到的阻力、滑轮(含挂钩)的质量和大小,不考虑钢索桥的摆动及形变.g取10m/s2.求:(1)若参赛者要达到B点,则人在A点处抓住挂钩时至少应具有的初动能;
(2)某次比赛规定参赛者须落在与钢丝绳最低点水平相距为d=2m、宽度a=1.6m,厚度不计的海绵垫子上.参赛者在A点抓住挂钩时应具有的初动能范围.
分析 (1)从A点静止滑下,最远能滑到C点,可知C点的速度为0.对A到C过程运用动能定理,有重力做功,摩擦力做功,动能的变化为0,求出摩擦力.对A到B运用动能定理,重力不做功,摩擦力做负功,根据动能定理求出初动能.
(2)参赛者在钢丝绳最低点脱钩后,做平抛运动,根据平抛运动的水平位移4a≤x≤5a,求出最低点的速度范围,然后对A到最低点运用动能定理,求出在A点初动能的范围.
解答 解:(1)根据动能定理,参赛者在A到C的过程中满足:mgh-Ff(L-L′)=0
则滑轮受到的阻力:Ff=$\frac{mgh}{L-L′}$=$\frac{60×10×0.1}{10-2}$N=7.5N
初动能为:EK=FfL=7.5×10J=75J
(2)从最底松开挂钩落到海绵垫上,所应具有的速度应为v,则:
H=$\frac{1}{2}g{t}^{2}$
得:t=$\sqrt{\frac{2H}{g}}$=0.8s
最小速度为:vmin=$\frac{d}{t}$=2.5m/s
最大速度为:vmax=$\frac{d+a}{t}$=4.5m/s
根据功能关系:EK+mgH1-Ff•$\frac{L}{2}$=$\frac{1}{2}$mv2
得:Ekmax=$\frac{1}{2}$mv2-mgH1+Ff$\frac{L}{2}$=465J
同理得:Ekmin=45J
故:45J<Ek<465J
答:
(1)若参赛者要达到B点,则人在A点处抓住挂钩时至少应具有的初动能为75J;
(2)某次比赛规定参赛者须在钢丝绳最低点水平相距为d=2m、宽度a=1.6m,厚度不计的海绵垫子上.参赛者在A点抓住挂钩时应具有的初动能范围为45J<Ek<465J
点评 解决本题的关键是恰当地选择研究过程,根据动能定理W合=△EK进行求解,要注意挖掘隐含的临界条件.


| A. | 质点甲、乙的速度相同 | |
| B. | 质点甲向所选定的正方向运动,质点乙与甲的运动方向相反 | |
| C. | 在相同的时间内,质点甲、乙的位移相同 | |
| D. | 不管质点甲、乙是否从同一地点开始运动,它们之间的距离一定越来越大 |
 如图所示,质量m=0.2kg的小物体从斜面A点以一定的初速度沿斜面滑下,在B点没有动能损失,水平面BC在C点与光滑半圆轨道CD平滑连接,D是最高点,小物体与AB、BC面的动摩擦因数均为μ=0.25,AB的长度L=5m,AB的倾斜角为37°,BC的长度s=8m,CD为半圆轨道的直径,CD的长度d=3m,不计空气阻力.(sin37°=0.6,cos37°=0.8)
如图所示,质量m=0.2kg的小物体从斜面A点以一定的初速度沿斜面滑下,在B点没有动能损失,水平面BC在C点与光滑半圆轨道CD平滑连接,D是最高点,小物体与AB、BC面的动摩擦因数均为μ=0.25,AB的长度L=5m,AB的倾斜角为37°,BC的长度s=8m,CD为半圆轨道的直径,CD的长度d=3m,不计空气阻力.(sin37°=0.6,cos37°=0.8) 如图所示,平面直角坐标系xoy,第一象限存在匀强电场,电场方向与x轴正方向夹角为60°,在边长为L的正三角形PQR范围内存在匀强磁场,PR与y轴重合,Q点在x轴上,磁感应强度为B,方向垂直纸面向里.一束包含各种速率带正电粒子由Q点沿x轴正方向射入磁场,粒子质量为m,电量为q,重力不计.
如图所示,平面直角坐标系xoy,第一象限存在匀强电场,电场方向与x轴正方向夹角为60°,在边长为L的正三角形PQR范围内存在匀强磁场,PR与y轴重合,Q点在x轴上,磁感应强度为B,方向垂直纸面向里.一束包含各种速率带正电粒子由Q点沿x轴正方向射入磁场,粒子质量为m,电量为q,重力不计. 如图所示,位于竖直平面上有$\frac{1}{4}$圆弧的光滑轨道,半径为R,OB沿竖直方向,A点距地面的竖直高度为H,把质量为m的钢球从A点由静止释放,最后落在了水平面上的C点处,已知重力加速度为g,不计空气阻力,求:
如图所示,位于竖直平面上有$\frac{1}{4}$圆弧的光滑轨道,半径为R,OB沿竖直方向,A点距地面的竖直高度为H,把质量为m的钢球从A点由静止释放,最后落在了水平面上的C点处,已知重力加速度为g,不计空气阻力,求: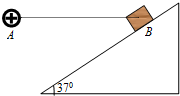 如图所示,在倾角为θ=37°的绝缘粗糙斜面上B处有质量为m=1kg、电荷量为q=+8×10-5C的物体(可视为质点);在和斜面处于同一平面内、B点等高处、相距r=3m的A点固定带电荷量Q=+1.6×10-4C的点电荷;现发现物体在斜面上处于静止状态.(重力加速度g=10m/s2,静电力常量k=9.0×109N.m2/C2,sin37°=0.6)
如图所示,在倾角为θ=37°的绝缘粗糙斜面上B处有质量为m=1kg、电荷量为q=+8×10-5C的物体(可视为质点);在和斜面处于同一平面内、B点等高处、相距r=3m的A点固定带电荷量Q=+1.6×10-4C的点电荷;现发现物体在斜面上处于静止状态.(重力加速度g=10m/s2,静电力常量k=9.0×109N.m2/C2,sin37°=0.6) 如图所示,O点距水平地面高度为H=3m,不可伸长的细线一端固定在O点另一端系一质量m=2kg的小球(可视为质点),另一根水平细线OA一端固定在墙上A点,细线OB与竖直方向的夹角θ=37°,l<lAB,且l<H,g取10m/s2,空气阻力不计.(sin37°=0.6,cos37°=0.8,结果可用根式表示.)
如图所示,O点距水平地面高度为H=3m,不可伸长的细线一端固定在O点另一端系一质量m=2kg的小球(可视为质点),另一根水平细线OA一端固定在墙上A点,细线OB与竖直方向的夹角θ=37°,l<lAB,且l<H,g取10m/s2,空气阻力不计.(sin37°=0.6,cos37°=0.8,结果可用根式表示.)