题目内容
18.在做某个精密的科学实验时,要求把容积为0.5L的容器内的气压降到1.0×102Pa以下.现在用一只最大容积也是0.5L的抽气机给它抽气.已知开始时容器中封闭气体的压强为1.0×105Pa.求:(1)至少抽多少次气才能达到实验要求?
(2)若室温为27℃,当抽气次数等于上问求出的最少次数时,容器内剩余空气的分子数是多少?
分析 (1)抽气过程气体发生等温变化,应用玻意耳定律可以求出抽气的次数.
(2)应用玻意耳定律求出标准状况下气体的体积,然后求出气体分子个数.
解答 解:(1)抽气过程气体发生等温变化,由玻意耳定律得:
第一次抽气过程:p0V=p1•2V,解得:p1=$\frac{1}{2}$p0,
第二次抽气过程:p1V=p2•2V,解得:p2=$\frac{1}{2}$p1=($\frac{1}{2}$)2p0,
第三次抽气过程:p2V=p3•2V,解得:p3=$\frac{1}{2}$p2=($\frac{1}{2}$)3p0,
…
第n次抽气过程:p(n-1)V=pn•2V,解得:pn=$\frac{1}{2}$p(n-1)=($\frac{1}{2}$)np0,
由题意可知:p0=1.0×105Pa,pn=1.0×102Pa,解得:n≈10次;
(2)容器内气体的状态参量:p=1.0×102Pa,V=0.5L,T=273+27=300K,
标准状况下气体状态参量:p0=1.0×105Pa,T0=273K,V0=?
由理想气体状态方程得:$\frac{pV}{T}$=$\frac{{p}_{0}{V}_{0}}{{T}_{0}}$,
容器内气体分子数:n=$\frac{{V}_{0}}{{V}_{mol}}{N}_{A}$,
解得:n=1.2×1019个;
答:(1)至少抽10次气才能达到实验要求;
(2)若室温为27℃,当抽气次数等于上问求出的最少次数时,容器内剩余空气的分子数是1.2×1019个.
点评 本题考查了求抽气次数、求分子个数问题,知道抽气过程气体发生等温变化是解题的关键,应用玻意耳定律、理想气体状态方程可以解题,解题时注意数学归纳法的应用.

练习册系列答案
相关题目
8.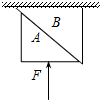 如图所示,物块B靠着水平天花板.物块A靠着B,在竖直向上的力F作用下,A、B保持静止,B与天花板间的动摩擦因数为μ,将F增大一些后(方向不变),A、B仍静止.下列判断正确的是( )
如图所示,物块B靠着水平天花板.物块A靠着B,在竖直向上的力F作用下,A、B保持静止,B与天花板间的动摩擦因数为μ,将F增大一些后(方向不变),A、B仍静止.下列判断正确的是( )
 如图所示,物块B靠着水平天花板.物块A靠着B,在竖直向上的力F作用下,A、B保持静止,B与天花板间的动摩擦因数为μ,将F增大一些后(方向不变),A、B仍静止.下列判断正确的是( )
如图所示,物块B靠着水平天花板.物块A靠着B,在竖直向上的力F作用下,A、B保持静止,B与天花板间的动摩擦因数为μ,将F增大一些后(方向不变),A、B仍静止.下列判断正确的是( )| A. | μ必定不为零 | |
| B. | μ可能为零 | |
| C. | 物块B原来可能受3个力,后来必定受4个力 | |
| D. | 物块B原来可能受3个力,后来可能受5个力 |
9.关于磁场和磁感线的描述,下列说法正确的是( )
| A. | 磁极之间的相互作用是通过磁场发生的,磁场和电场一样,也是客观存在的特殊物质 | |
| B. | 磁感线用来形象地描写磁场中各点的磁场的强弱和方向 | |
| C. | 磁感线是从磁铁的N极出发,终止于S极 | |
| D. | 磁感线是闭合的环形线,总是环绕电流而存在 |
3. 如图所示,两根直木棍AB和CD相互平行,固定在同一个水平面上.一个光滑的圆柱形工件 P静止架在两木棍之间,若保持两个个木棍在同一个水平面内,而将他们之间的距离减小稍许,则工件P再次静止时受到木棍AB的支持力与原来相比( )
如图所示,两根直木棍AB和CD相互平行,固定在同一个水平面上.一个光滑的圆柱形工件 P静止架在两木棍之间,若保持两个个木棍在同一个水平面内,而将他们之间的距离减小稍许,则工件P再次静止时受到木棍AB的支持力与原来相比( )
 如图所示,两根直木棍AB和CD相互平行,固定在同一个水平面上.一个光滑的圆柱形工件 P静止架在两木棍之间,若保持两个个木棍在同一个水平面内,而将他们之间的距离减小稍许,则工件P再次静止时受到木棍AB的支持力与原来相比( )
如图所示,两根直木棍AB和CD相互平行,固定在同一个水平面上.一个光滑的圆柱形工件 P静止架在两木棍之间,若保持两个个木棍在同一个水平面内,而将他们之间的距离减小稍许,则工件P再次静止时受到木棍AB的支持力与原来相比( )| A. | 偏大 | B. | 偏小 | ||
| C. | 不变 | D. | 条件不足,无法判断 |
7.在“验证机械能守恒定律”实验中,下列叙述中正确的是( )
| A. | 必须要用天平测出重锤的质量 | |
| B. | 实验时要先闭合打点计时器的电源开关,再释放重锤 | |
| C. | 打出的纸带中,只要点迹清晰,就可用公式mg△h=$\frac{1}{2}$mv2来验证机械能是否守恒 | |
| D. | 验证机械能是否守恒必须先确定重力势能的参考平面 |
8.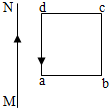 通电矩形线圈abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab边与MN平行,关于MN 的磁场对线圈的作用,下列说法中正确的是( )
通电矩形线圈abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab边与MN平行,关于MN 的磁场对线圈的作用,下列说法中正确的是( )
 通电矩形线圈abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab边与MN平行,关于MN 的磁场对线圈的作用,下列说法中正确的是( )
通电矩形线圈abcd与无限长通电直导线MN在同一平面内,电流方向如图所示,ab边与MN平行,关于MN 的磁场对线圈的作用,下列说法中正确的是( )| A. | 线框的四条边中有两条边所受的安培力方向相同 | |
| B. | 线框四条边中有两条边所受的安培力大小相等 | |
| C. | 线框所受的安培力的合力方向向左 | |
| D. | 线框所受的安培力的合力方向向右 |
 如图所示,水平桌面上有A、B是两个相同的、重量为G的圆形滑块,它们与桌面的动摩擦因素均为μ.现用一根轻绳将A、B相连,并用一个水平力F作用在绳子的中点.绳子被拉紧时,作用点两边绳子的夹角为120°,F沿绳子夹角的角平分线方向.则F的大小至少为μG时,才能将A、B拉动.
如图所示,水平桌面上有A、B是两个相同的、重量为G的圆形滑块,它们与桌面的动摩擦因素均为μ.现用一根轻绳将A、B相连,并用一个水平力F作用在绳子的中点.绳子被拉紧时,作用点两边绳子的夹角为120°,F沿绳子夹角的角平分线方向.则F的大小至少为μG时,才能将A、B拉动.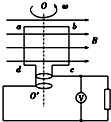 如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,转速n=5r/s,外电路电阻R=4Ω,求:
如图所示,匀强磁场的磁感应强度B=0.5T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,转速n=5r/s,外电路电阻R=4Ω,求: