题目内容
【题目】(1)科学家发现,除了类似太阳系的恒星-行星系统,还存在许多双星系统,通过对它们的研究,使我们对宇宙有了较深刻的认识。双星系统是由两个星体构成,其中每个星体的线度(直径)都远小于两星体间的距离,一般双星系统距离其他星体很远,可以当做孤立系统处理。已知某双星系统中每个星体的质量都是M0,两者相距L,它们正围绕两者连线的中点做匀速圆周运动,引力常量为G。 求:
①该双星系统中星体的加速度大小a;
②该双星系统的运动周期T。
(2)微观世界与宏观世界往往存在奇妙的相似性。对于氢原子模型,因为原子核的质量远大于电子质量,可以忽略原子核的运动,形成类似天文学中的恒星-行星系统,记为模型Ⅰ。另一种模型认为氢原子的核外电子并非绕核旋转,而是类似天文学中的双星系统,核外电子和原子核依靠库仑力作用使它们同时绕彼此连线上某一点做匀速圆周运动,记为模型Ⅱ。已知核外电子的质量为m,氢原子核的质量为M,二者相距为r,静电力常量为k,电子和氢原子核的电荷量大小均为e。
①模型Ⅰ、Ⅱ中系统的总动能分别用EkⅠ、 EkⅡ表示,请推理分析,比较EkⅠ、 EkⅡ的大小关系;
②模型Ⅰ、Ⅱ中核外电子做匀速圆周运动的周期分别用TⅠ、TⅡ表示,通常情况下氢原子的研究采用模型Ⅰ的方案,请从周期的角度分析这样简化处理的合理性。
【答案】(1) ①![]() ②
②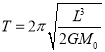 (2) ①
(2) ①![]() ②
②![]() ,因为M>>m,可得TⅠ≈TⅡ,所以采用模型Ⅰ更简单方便。
,因为M>>m,可得TⅠ≈TⅡ,所以采用模型Ⅰ更简单方便。
【解析】(1)①根据万有引力定律和牛顿第二定律有: ![]()
解得![]() ②
②
②由运动学公式可知, ![]()
解得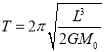
(2)①模型Ⅰ中,设电子和原子核的速度分别为v对于电子绕核的运动,根据库仑定律和牛顿第二定律有![]()
解得: ![]()
模型Ⅱ中,设电子和原子核的速度分别为v1、v2,电子的运动半径为r1,原子核的运动半径为r2。根据库仑定律和牛顿第二定律
对电子有: ![]() ,解得
,解得![]()
对于原子核有: ![]() ,解得
,解得![]()
系统的总动能:EkⅡ=Ek1+ Ek2=![]()
即在这两种模型中,系统的总动能相等。
②模型Ⅰ中,根据库仑定律和牛顿第二定律有
![]() ,解得
,解得![]()
模型Ⅱ中,电子和原子核的周期相同,均为TⅡ
根据库仑定律和牛顿第二定律
对电子有 ![]() , 解得
, 解得![]()
对原子核有 ![]() , 解得
, 解得![]()
因r1+r2=r,将以上两式代入,可解得![]()
所以有 ![]()
因为M>>m,可得TⅠ≈TⅡ,所以采用模型Ⅰ更简单方便。

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案