题目内容
质谱仪是一种测定带电粒子质量和分析同位素的重要工具，它的构造原理如图所示。离子源S产生质量为m、带电量为q的某种正离子，离子产生出来时速度很小，可以看作是静止的。粒子从容器A下方小孔S1飘入电势差为U的加速电场，然后经过小孔S2和S3后沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中，最后打到照相底片D上。
(1)小孔S1和S2处的电势比较，哪处的高？
在小孔S1和S2处的电势能，哪处高？如果容器A接地且电势为0，则小孔S1和S2处的电势各为多少？(设小孔极小，其电势和小孔处的电极板的电势相同)
(2)求粒子进入磁场时的速率和粒子在磁场中运动的轨道半径。
(3)如果从容器下方的S1小孔飘出的是具有不同的质量的带电量为q的正离子，那么这些粒子打在照相底片的同一位置，还是不同位置？如果是不同位置，那么质量分别为
的粒子在照相底片的排布等间距吗？写出说明。
解析：(1)由于电荷量为带正电的粒子，从容器下方的S1小孔飘入电势差为U的加速电场，要被加速，S1和S2处的电势比较，S1处的高，从小孔S1到S2电场力做正功，电势能减小，所以粒子在小孔S1处的电势能高于在S2处。如果容器A接地且电势为0，而小孔S1和S2处的电势差为U，所以小孔S1和S2处的电势各为0和-U。
(2)设从容器下方的S1小孔飘出的是具有不同的质量的电荷量为的粒子，到达S2的速度为v，经S3进入射入磁场区，根据能量守恒，有
v=
设粒子在洛伦兹力作用下做匀速圆周运动的半径为R，由洛伦兹力公式和牛顿定律得：
(3)在磁场中偏转距离d=
由于是具有不同的质量的粒子，所以距离d不同，这些粒子打在照相底片的不同位置。从上式可以看出，在磁场中偏转距离d与质量的平方根成正比，所以质量分别为的粒子在照相底片的排布间距不等。
新思维假期作业暑假吉林大学出版社系列答案
质谱仪是一种测定带电粒子质量和分析同位素的重要工具，它的构造原理如图所示，离子源S产生的各种不同正离子束（电量为q，速度可看作为零），经加速电场电压U加速后垂直进入有界匀强磁场，到达记录它的照相底片P上，设离子在P上的位置到入口处S1的距离为x，不计离子重力，则下列说法正确的是（ ）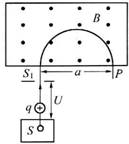
质谱仪是一种测定带电粒子质量和分析同位素的重要工具．它的构造原理如图所示，离子源S产生带电量为q的某种正离子，离子射出时的速度很小，可以看作是静止的，离子经过电压U加速后形成离子束流，然后垂直于磁场方向进入磁感应强度为B的匀强磁场，沿着半圆周运动而到达记录它的照相底片P上．实验测得：它在P上的位置到入口处S1的距离为a，离子束流的电流为I．请回答下列问题：
质谱仪是一种测定带电粒子质量和分析同位素的重要工具，它的构造原理如图所示，离子源S产生的各种不同正离子束（速度可看作为零），经加速电场加速后垂直进入有界匀强磁场，到达记录它的照相底片P上，设离子在P上的位置到入口处S1的距离为x，则下列判断正确的是（ ）
质谱仪是一种测定带电粒子质量或分析同位素的重要设备，它的构造原理如图所示．离子源S产生的各种不同正离子束（速度可视为零），经MN间的加速电压U加速后从小孔S1垂直于磁感线进入匀强磁场，运转半周后到达照相底片上的P点．设P到S1的距离为x，则（ ）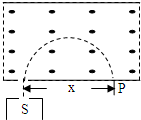
质谱仪是一种测定带电粒子质量和分析同位素的重要工具，它的构造原理如图所示，离子源S可以发出各种不同的正离子束，离子从S出来时速度很小，可以看作是静止的，离子经过加速电场加速后垂直进入有界匀强磁场（图中线框所示），并沿着半圆周运动而到达照像底片上的P点，测得P点到入口处S的距离为x?（ ）