题目内容
13. 质量和带电量都相同的两个粒子,以不同的速率垂直于磁感线方向射入匀强磁场中,两粒子的运动轨迹如图中①、②所示,粒子的重力不计,下列对两个粒子的运动速率υ和在磁场中运动时间t及运动周期T、角速度的说法中正确的是( )
质量和带电量都相同的两个粒子,以不同的速率垂直于磁感线方向射入匀强磁场中,两粒子的运动轨迹如图中①、②所示,粒子的重力不计,下列对两个粒子的运动速率υ和在磁场中运动时间t及运动周期T、角速度的说法中正确的是( )| A. | υ1<υ2 | B. | t1<t2 | C. | T1>T2 | D. | ω1=ω2 |
分析 粒子垂直进入匀强磁场中由洛伦兹力提供向心力做匀速圆周运动,周期为T=$\frac{2πm}{qB}$,半径为r=$\frac{mv}{qB}$,两个粒子运动的周期和角速度相同.根据轨迹分析半径的大小,即可知速度的大小.
解答 解:
A、粒子垂直进入匀强磁场中由洛伦兹力提供向心力做匀速圆周运动,由轨迹和几何知识得知,半径关系为r1<r2,半径为r=$\frac{mv}{qB}$,两个粒子的质量和电量都相等,则得υ1<υ2,故A正确.
B、由轨迹看出,轨迹对应的圆心角大小关系为:θ1>θ2,粒子在磁场中运动时间为t=$\frac{θ}{2π}T$,两个粒子运动的周期相同,则t1>t2.故B错误.
C、D粒子匀速圆周运动的周期为T=$\frac{2πm}{qB}$,两个粒子的质量和电量都相等,周期相同,又角速度ω=$\frac{2π}{T}$,则得角速度也相同.故C错误,D正确.
故选:AD
点评 本题是带电粒子在匀强磁场中匀速圆周运动的问题,掌握半径公式r=$\frac{mv}{qB}$和周期公式T=$\frac{2πm}{qB}$是解答的基础.粒子运动时间与圆心角的大小成正比.

练习册系列答案
相关题目
3.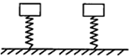 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )| A. | 两物块达最大速度时的高度相同 | B. | 上升的最大高度不同 | ||
| C. | 最大加速度相同 | D. | 最大重力势能不同 |
8.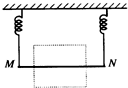 如图所示,一根金属棒MN,两端用弹簧悬挂于天花板上,棒中通有方向从M流向N的电流.若在图中的虚线范围内加一磁场,可以使弹簧的弹力增大(弹力的方向不变).关于该磁场的方向,以下判断中正确的是( )
如图所示,一根金属棒MN,两端用弹簧悬挂于天花板上,棒中通有方向从M流向N的电流.若在图中的虚线范围内加一磁场,可以使弹簧的弹力增大(弹力的方向不变).关于该磁场的方向,以下判断中正确的是( )
 如图所示,一根金属棒MN,两端用弹簧悬挂于天花板上,棒中通有方向从M流向N的电流.若在图中的虚线范围内加一磁场,可以使弹簧的弹力增大(弹力的方向不变).关于该磁场的方向,以下判断中正确的是( )
如图所示,一根金属棒MN,两端用弹簧悬挂于天花板上,棒中通有方向从M流向N的电流.若在图中的虚线范围内加一磁场,可以使弹簧的弹力增大(弹力的方向不变).关于该磁场的方向,以下判断中正确的是( )| A. | 垂直纸面向里 | B. | 垂直纸面向外 | C. | 平行纸面向上 | D. | 平行MN向左 |
18.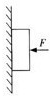 如图所示,用力F把木块紧压在竖直墙上不动,木块对墙的压力为N木块受到的摩擦力为f,到的重力为G,则( )
如图所示,用力F把木块紧压在竖直墙上不动,木块对墙的压力为N木块受到的摩擦力为f,到的重力为G,则( )
 如图所示,用力F把木块紧压在竖直墙上不动,木块对墙的压力为N木块受到的摩擦力为f,到的重力为G,则( )
如图所示,用力F把木块紧压在竖直墙上不动,木块对墙的压力为N木块受到的摩擦力为f,到的重力为G,则( )| A. | N>F | B. | N<F | C. | f>G | D. | f=G |
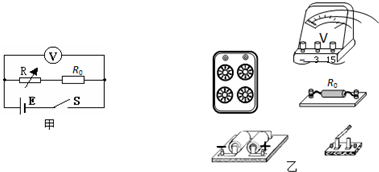
5.如图表示交变电流随时间变化图象,则交变电流有效值为( )


| A. | 3$\sqrt{2}$A | B. | 3A | C. | 2$\sqrt{3}$A | D. | 3.5A |
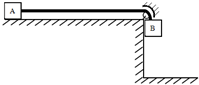 如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求:
如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求: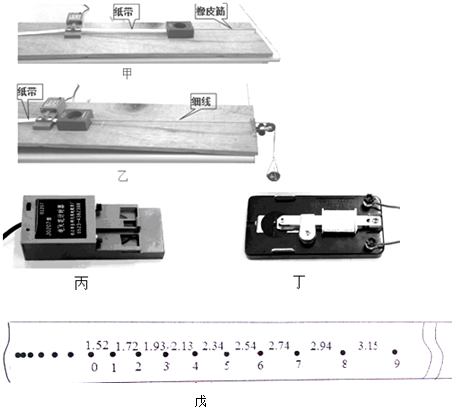
 如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小车足够长.求:
如图所示,质量M=8kg的小车放在水平光滑的平面上,在小车左端加一水平推力F=8N,当小车向右运动的速度达到1.5m/s时,在小车前端轻轻地放上一个大小不计,质量为m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,小车足够长.求: