题目内容
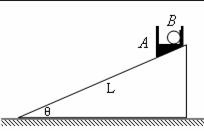
 倾角为θ的固定斜面顶端有一滑轮,细线跨过滑轮连接A、B两个质量均为m的物块.让A物块静止在斜面底端,拉A的细线与斜面平行,B物块悬挂在离地面h高处,如图所示.斜面足够长,物块与斜面间的动摩擦因数为μ,不计其它阻力.释放后B物块下落A物块沿斜面上滑.
倾角为θ的固定斜面顶端有一滑轮,细线跨过滑轮连接A、B两个质量均为m的物块.让A物块静止在斜面底端,拉A的细线与斜面平行,B物块悬挂在离地面h高处,如图所示.斜面足够长,物块与斜面间的动摩擦因数为μ,不计其它阻力.释放后B物块下落A物块沿斜面上滑.某同学在计算A物块沿斜面上滑的时间时,解题方法如下:
运用动能定理求B物块落地时A物块的速度v.
mgh(1-sinθ-μcosθ)=
| mv2 |
| 2 |
运用牛顿第二定律求A的加速度a.
mg (1-sinθ-μcosθ)=ma,从中解出a;
A物块沿斜面上滑的时间t=
| v |
| a |
你认为该同学的解法是否有错?如有错误请指出错在哪里,并列出相应正确的求解表达式(不必演算出最后结果).
分析:本题有三个要求:首先判断该同学是否有错误,再指出错误错在哪里,第三列出相应正确的求解表达式.释放后B物块下落过程中,B向下做加速运动,细线的拉力小于B的重力.动能定理的研究对象是AB系统,方程两边质量应是2m.再分析动能定理和牛顿第二定律列式中的错误.
解答:解:该同学的解法有三处错误:一是运用动能定理时,研究对象是AB组成的系统,等式右边的质量应该是AB的总质量2m而不是m.
正确的表达式为 mgh(1-sinθ-μcosθ)=
?2mv2;
二是运用牛顿第二定律时,等式右边的质量应该是AB的总质量2m而不是m.
正确的表达式为 mg(1-sinθ-μcosθ)=2ma
三是求A物块沿斜面上滑的时间有错,A物块达速度v后还要减速上滑,该同学漏掉了这一段时间.
正确的表达应该是 减速上滑时的加速度为a′=g(sinθ+μcosθ)
减速上滑时的时间为t′=
整个上滑的时间应该为 t=
+
.
正确的表达式为 mgh(1-sinθ-μcosθ)=
| 1 |
| 2 |
二是运用牛顿第二定律时,等式右边的质量应该是AB的总质量2m而不是m.
正确的表达式为 mg(1-sinθ-μcosθ)=2ma
三是求A物块沿斜面上滑的时间有错,A物块达速度v后还要减速上滑,该同学漏掉了这一段时间.
正确的表达应该是 减速上滑时的加速度为a′=g(sinθ+μcosθ)
减速上滑时的时间为t′=
| v |
| a′ |
整个上滑的时间应该为 t=
| v |
| a |
| v |
| a′ |
点评:本题是评价题解答要完整,不能遗漏,有三个要求:一判断正误;二指出错误所在;三是写出正确解答.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
如图所示,一物体自倾角为θ的固定斜面顶沿水平方向抛出后落在斜面上.物体与斜面接触时速度与水平方向的夹角φ满足( )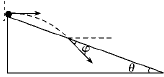
| A.tanφ=sinθ | B.tanφ=cosθ |
| C.tanφ=tanθ | D.tanφ=2tanθ |
 如图所示是一种简易“千斤顶”.一竖直放置的T形轻杆由于光滑限制套管P的作用,使它只能在竖直方向上运动.若轻杆上端放一质量M=100kg的物体,轻杆的下端通过一与杆固定连接的小轮放在倾角为θ=37°的斜面体上,并将斜面体放在光滑水平面上.现沿水平方向对斜面体施以推力F,(小轮与斜面体的摩擦和质量不计,g=10m/s2)
如图所示是一种简易“千斤顶”.一竖直放置的T形轻杆由于光滑限制套管P的作用,使它只能在竖直方向上运动.若轻杆上端放一质量M=100kg的物体,轻杆的下端通过一与杆固定连接的小轮放在倾角为θ=37°的斜面体上,并将斜面体放在光滑水平面上.现沿水平方向对斜面体施以推力F,(小轮与斜面体的摩擦和质量不计,g=10m/s2) 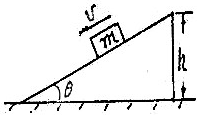 如图所示,物体的质量m=1kg,恰好能沿倾角为θ=370、高为h=2m的固定斜面匀速滑下,现用沿斜面向上的恒力F推物体,使物体m从静止开始,由斜面底端沿斜面推到顶端,经历时间t=4s,(sin37°=0.6,cos37°=0.8)求:
如图所示,物体的质量m=1kg,恰好能沿倾角为θ=370、高为h=2m的固定斜面匀速滑下,现用沿斜面向上的恒力F推物体,使物体m从静止开始,由斜面底端沿斜面推到顶端,经历时间t=4s,(sin37°=0.6,cos37°=0.8)求: